
| 3 |
| x |
| 2 |
| A、[-1,3] |
| B、(-1,2)∪(2,3) |
| C、(-1,3) |
| D、[-1,2)∪(2,3] |
| 3 |
| x |
| 2 |
| 3 |
| π |
| 6 |
| π |
| 6 |
| a-1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 13π |
| 6 |
| 3 |
| x |
| 2 |
| a-1 |
| 2 |
| a-1 |
| 2 |
| 1 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
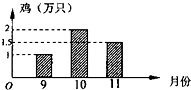 为了了解“预防禽流感疫苗”的使用情况,某市卫生部门对本地区9月份至11月份注射疫苗的所有养鸡场进行了调查.表格表示每个月所调查的养鸡场的个数,如图表示三个月中各养鸡场注射了疫苗的鸡的数量的平均数.根据图表提供的信息,可以得出这三个月本地区每月注射了疫苗的鸡的数量平均为
为了了解“预防禽流感疫苗”的使用情况,某市卫生部门对本地区9月份至11月份注射疫苗的所有养鸡场进行了调查.表格表示每个月所调查的养鸡场的个数,如图表示三个月中各养鸡场注射了疫苗的鸡的数量的平均数.根据图表提供的信息,可以得出这三个月本地区每月注射了疫苗的鸡的数量平均为| 月份 | 养鸡场(个数) |
| 9 | 20 |
| 10 | 50 |
| 11 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| A、abcd∈[0,e4) | ||||
B、a+b+c+d∈[e5+
| ||||
C、若关于x的方程f(x)+x=m恰有三个不同实根,则m必有一个取值为
| ||||
| D、若关于x的方程f(x)+x=m恰有三个不同实根,则m取值唯一 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、(-1,6) |
| B、[-1,6] |
| C、(-∞,-1)∪(6,+∞) |
| D、(-∞,-1]∪[6,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某市一公交线路某区间内共设置六个站点(如图所示),分别为A0,A1,A2,A3,A4,A5,现有甲、乙两人同时从A0站点上车,且他们中的每个人在站点Ai(i=1,2,3,4,5)下车是等可能的.则甲、乙两人不在同一站点下车的概率为( )
某市一公交线路某区间内共设置六个站点(如图所示),分别为A0,A1,A2,A3,A4,A5,现有甲、乙两人同时从A0站点上车,且他们中的每个人在站点Ai(i=1,2,3,4,5)下车是等可能的.则甲、乙两人不在同一站点下车的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com