Question

18．已知圆C：x²+y²=2，点A（-2，0）及点B（3，a），从A点观察B点，若视线被圆C挡住，则a的取值范围是（5，+∞）∪（-∞，-5）．

Answer 1

分析 先设过A的直线方程为：kx-y+2k=0，根据“使视线不被圆C挡住”则找到直线与圆相切的位置，这样，先求得圆心到直线的距离，再让其等于半径，求得切线方程，再令x=4得y=±5，从而求得实数a的取值范围．

解答 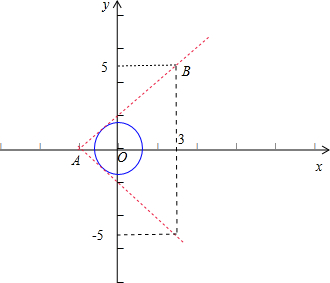解：已知圆C：x² +y² =2，表示以（0，0）为圆心、半径等于$\sqrt{2}$的圆，
又点A（-2，0）及点B（3，a），
设过A的圆的切线方程为：kx-y+2k=0，根据圆心（0，0）到直线的距离 d=$\frac{|0-0+2k|}{\sqrt{{k}^{2}+1}}$=$\sqrt{2}$．
解得k=±1，故圆的过点A（-2，0）的切线方程为 y=±（x+2）．
再把x=3代入圆的切线方程求得y=±5，
故要使视线不被圆C挡住，则实数a的取值范围是 （5，+∞）∪（-∞，-5），
故答案为：（5，+∞）∪（-∞，-5）．

点评 本题主要考查直线与圆的位置关系，作为相切是研究相交和相离的关键位置，应熟练掌握，属于中档题．