
分析 (I)法一:由已知等式及正弦定理,得2sinBcosA=sinB,结合sinB≠0,A∈(0,π),可得A的值.
法二:由已知等式及余弦定理,得$cosA=\frac{{{b^2}+{c^2}-{a^2}}}{2bc}=\frac{1}{2}$,结合范围A∈(0,π),即可求A的值.
(II)由(I)及正弦定理得$b=2\sqrt{3}sinB;c=2\sqrt{3}sinC$,可得△ABC的周长$l=3+2\sqrt{3}{sinB}+2\sqrt{3}sin(B+\frac{π}{3})$=$3+6sin(B+\frac{π}{6})$,结合范围$B∈(0,\frac{2π}{3})$,即可求△ABC的周长最大值.
解答 (本小题满分12分)
(I)解:法一:由(2b-c)cosA=acosC及正弦定理,得(2sinB-sinC)cosA=sinAcosC,…(3分)
∴2sinBcosA=sinCcosA+sinAcosC,
∴2sinBcosA=sin(C+A)=sinB,
∵B∈(0,π),
∴sinB≠0,
∵A∈(0,π),
$cosA=\frac{1}{2}$,
∴$A=\frac{π}{3}$…(6分)
法二:由(2b-c)cosA=acosC及余弦定理,得$(2b-c)\frac{{{b^2}+{c^2}-{a^2}}}{2bc}=a\frac{{{b^2}+{a^2}-{c^2}}}{2ba}$,…(3分)
整理,得b2+c2-a2=bc,可得:$cosA=\frac{{{b^2}+{c^2}-{a^2}}}{2bc}=\frac{1}{2}$,
∵A∈(0,π),
∴$A=\frac{π}{3}$.…(6分)
(II)解:由(I)得∴$A=\frac{π}{3}$,由正弦定理得$\frac{b}{sinB}=\frac{c}{sinC}=\frac{a}{sinA}=\frac{3}{{\frac{{\sqrt{3}}}{2}}}=2\sqrt{3}$,
所以$b=2\sqrt{3}sinB;c=2\sqrt{3}sinC$,
△ABC的周长:$l=3+2\sqrt{3}{sinB}+2\sqrt{3}sin(B+\frac{π}{3})$,…(9分)
=$3+2\sqrt{3}{sinB}+2\sqrt{3}({sinBcos}\frac{π}{3}+cosBsin\frac{π}{3})$
=$3+3\sqrt{3}{sinB}+3cosB$
=$3+6sin(B+\frac{π}{6})$,
∵$B∈(0,\frac{2π}{3})$,
当$B=\frac{π}{3}$时,△ABC的周长取得最大值为9.…(12分)
点评 本题主要考查了正弦定理,余弦定理,三角函数恒等变换的应用,正弦函数的图象和性质在解三角形中的综合应用,考查了转化思想和数形结合思想,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{5}{3}$ | C. | $\frac{4}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
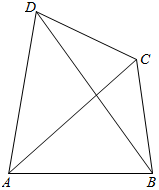 如图,平面四边形ABCD中,AB=$\sqrt{5}$,AD=2$\sqrt{2}$,CD=$\sqrt{3}$,∠CBD=30°,∠BCD=120°,求
如图,平面四边形ABCD中,AB=$\sqrt{5}$,AD=2$\sqrt{2}$,CD=$\sqrt{3}$,∠CBD=30°,∠BCD=120°,求查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 20 | 40 | 60 | 70 | 80 |
| A. | 210 | B. | 210.5 | C. | 211.5 | D. | 212.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p是真命题 | B. | 命题p的逆命题是真命题 | ||
| C. | 命题p的否命题是:若a<1,则a2≥1 | D. | 命题p的逆否命题是:若a2≥1,则a<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
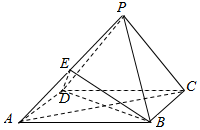 如图,在四棱锥P-ABCD中,底面为矩形,平面PCD丄平面ABCD,PC丄PD,PD=AD,E为PA的中点.
如图,在四棱锥P-ABCD中,底面为矩形,平面PCD丄平面ABCD,PC丄PD,PD=AD,E为PA的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com