Question

6．计算由曲线y²=x和直线y=x-2所围成的图形的面积是（　　）

• A． $\frac{11}{2}$
• B． 18
• C． $\frac{23}{6}$
• D． $\frac{9}{2}$

Answer 1

分析 先求出曲线y²=2x 和直线y=x-2的交点坐标，从而得到积分的上下限，然后利用定积分表示出图形面积，最后根据定积分的定义求出即可．

解答 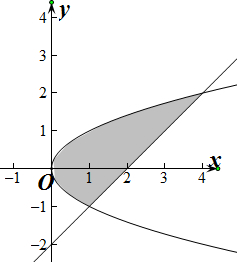解：联立方程组得$\left\{\begin{array}{l}{{y}^{2}=x}\\{y=x-2}\end{array}\right.$解得曲线y²=x和直线y=x-2的交点坐标为：（1，-1），（4，2），
选择y为积分变量，
∴由曲线y²=x和直线y=x-2所围成的图形的面积S=${∫}_{-1}^{2}$（y+2-y²）dy=$（\frac{1}{2}{y}^{2}+2y-\frac{1}{3}{y}^{3}）$|${\;}_{-1}^{2}$=（2+4-$\frac{8}{3}$）-（$\frac{1}{2}$-2+$\frac{1}{3}$）=$\frac{9}{2}$

点评 本题主要考查了定积分在求面积中的应用，以及会利用定积分求图形面积的能力．应用定积分求平面图形面积时，积分变量的选取是至关重要的，属于基础题．