
分析 (1)运用代入法,计算即可得到所求值;
(2)设an=kn+t,由an=2an-1+n(n>1,n∈N*).可得kn+t=2(kn-k+t)+n,由恒等知识,可得k=-1,t=-2,进而得到通项公式;
(3)假设{an}为等比数列,设an=kqn,代入条件,运用恒等知识,即可判断.
解答 解:(1)an=2an-1+n(n>1,n∈N*).
若a1=1,则a2=2a1+2=4,
a3=2a2+3=8+3=11,
a4=2a3+4=22+4=26;
(2)若{an}为等差数列,设an=kn+t,
由an=2an-1+n(n>1,n∈N*).
可得kn+t=2(kn-k+t)+n,
即有k=2k+1,t=2(t-k),
解得k=-1,t=-2,
则an=-n-2;
(3)假设{an}为等比数列,设an=kqn,
由an=2an-1+n(n>1,n∈N*).
可得kqn=2kqn-1+n,
若q=1,则k=-n,不恒成立;
若q≠1,则等式不恒成立.
故{an}不能为等比数列.
点评 本题考查等差数列和等比数列的通项公式的运用,考查运算和推理能力,属于中档题.


科目:高中数学 来源: 题型:解答题
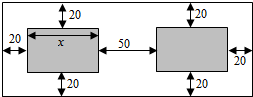 某单位因工作需要,要制作一批操作台面,台面上有两块大小相同的长方形钢化玻璃(图中阴影部分),每块钢化玻璃的面积为1800cm2,每块钢化玻璃需能放置半径为15cm的圆形器皿,每块钢化玻璃周围与操作台边缘要留20cm空白,两块钢化玻璃的间距为50cm,设钢化玻璃长为xcm,操作台面面积为S.
某单位因工作需要,要制作一批操作台面,台面上有两块大小相同的长方形钢化玻璃(图中阴影部分),每块钢化玻璃的面积为1800cm2,每块钢化玻璃需能放置半径为15cm的圆形器皿,每块钢化玻璃周围与操作台边缘要留20cm空白,两块钢化玻璃的间距为50cm,设钢化玻璃长为xcm,操作台面面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{23}{32}$ | B. | $\frac{23}{43}$ | C. | $\frac{29}{42}$ | D. | $\frac{21}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com