Question

17．已知O为坐标原点，F是双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的左焦点，A，B分别为双曲线C的左、右顶点，P为双曲线C上的一点，且PF⊥x轴，过点A的直线l与线段PF交于M，与y轴交于点E，直线BM与y轴交于点N，若|OE|=3|ON|，则双曲线C的离心率为（　　）

• A． $\frac{4}{3}$
• B． $\frac{3}{2}$
• C． 2
• D． 3

Answer 1

分析 根据条件分别求出直线AE和BN的方程，求出N，E的坐标，利用|OE|=3|ON|的关系建立方程进行求解即可．

解答 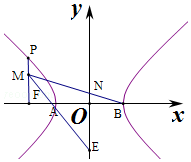解：因为PF⊥x轴，所以设M（-c，t），
则A（-a，0），B（a，0），AE的斜率$k=\frac{t}{a-c}$，
则AE的方程为$y=\frac{t}{a-c}（x+a）$，令x=0，则$y=\frac{ta}{a-c}$，
即$E（0，\frac{ta}{a-c}）$，
BN的斜率$k=-\frac{t}{a+c}$，则BN的方程为$y=-\frac{t}{a+c}（x-a）$，
令x=0，则$y=\frac{ta}{a+c}$，即$N（0，\frac{ta}{a+c}）$，
因为|OE|=3|ON|，所以$3|{\frac{ta}{a+c}}|=|{\frac{ta}{a-c}}|$，即$\frac{3}{a+c}=\frac{1}{c-a}$，
则3（c-a）=a+c，即c=2a，则离心率$e=\frac{c}{a}=2$．
故选C．

点评 本题主要考查双曲线离心率的计算，根据条件求出直线方程和点N，E的坐标是解决本题的关键．