
| A. | 2 | B. | $\frac{9}{5}$ | C. | 3 | D. | $-\frac{3}{5}$ |
分析 由$\overrightarrow a⊥\overrightarrow b$得$\overrightarrow{a}$•$\overrightarrow{b}$=0,求出sinα=2cosα,代入$\frac{{{{sin}^3}α+{{cos}^3}α}}{sinα-cosα}$计算即可.
解答 解:$\overrightarrow a=(4,-2),\overrightarrow b=(cosα,sinα)$,且$\overrightarrow a⊥\overrightarrow b$,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=4cosα-2sinα=0,
∴sinα=2cosα,且cosα≠0;
∴$\frac{{{{sin}^3}α+{{cos}^3}α}}{sinα-cosα}$=$\frac{{8cos}^{3}α{+cos}^{3}α}{2cosα-cosα}$
=9cos2α
=$\frac{{9cos}^{2}α}{{sin}^{2}α{+cos}^{2}α}$
=$\frac{{9cos}^{2}α}{{4cos}^{2}α{+cos}^{2}α}$
=$\frac{9}{5}$.
故选:B.
点评 本题考查了三角函数的化简与求值,考查了同角三角函数的基本关系式,是基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
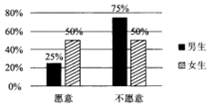 2017年1月1日,作为贵阳市打造“千园之城”27个示范性公元之一的泉湖公园正式开园,元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放,现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:
2017年1月1日,作为贵阳市打造“千园之城”27个示范性公元之一的泉湖公园正式开园,元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放,现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:| 愿意 | 不愿意 | 总计 | |
| 男生 | |||
| 女生 | |||
| 总计 |
| P(K2≥k0) | 0.1 | 0.05 | 0.025 | 0.01 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com