
| A. | $\frac{5}{4}$[1-($\frac{1}{5}$)n] | B. | $\frac{1}{4}$[1-($\frac{1}{5}$)n] | C. | $\frac{1}{4}$[1-($\frac{1}{5}$)n-1] | D. | $\frac{5}{4}$[1-($\frac{1}{5}$)n-1] |
分析 根据题意,由$\overrightarrow{a}$∥$\overrightarrow{b}$结合向量平行的坐标表示方法可得2an+1=$\frac{2}{5}$×an,即$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{1}{5}$,由等比数列的定义可得数列{an}为首项a1=1,公比为$\frac{1}{5}$的等比数列,由等比数列前n项和公式计算可得答案.
解答 解:根据题意,向量$\overrightarrow{a}$=(an,2),$\overrightarrow{b}$=(an+1,$\frac{2}{5}$),
若$\overrightarrow{a}$∥$\overrightarrow{b}$,则有2an+1=$\frac{2}{5}$×an,即$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{1}{5}$,
则数列{an}为首项a1=1,公比为$\frac{1}{5}$的等比数列,
则其前n项和为Sn=$\frac{1[1-(\frac{1}{5})^{n}]}{1-\frac{1}{5}}$=$\frac{5}{4}$[1-($\frac{1}{5}$)n],
故选:A.
点评 本题考查等比数列的前n项和,关键是由向量平行的坐标表示方法得到数列{an}为等比数列.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
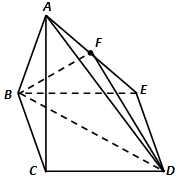 如图等边三角形ABC所在平面与菱形BCDE所在平面互相垂直,F为AE中点,AB=2,∠CBE=60°.
如图等边三角形ABC所在平面与菱形BCDE所在平面互相垂直,F为AE中点,AB=2,∠CBE=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若0<α<$\frac{π}{2}$,则sin α<tan α | |
| B. | 若α是第二象限角,则$\frac{α}{2}$为第一象限角或第三象限角 | |
| C. | 若角α的终边过点P(3k,4k)且k≠0,则sin α=$\frac{4}{5}$ | |
| D. | 若α=-$\frac{π}{3}$,则cos α=$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4-2ln2 | D. | 2-2ln2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 4 | B. | 4+4$\sqrt{2}$ | C. | 8+4$\sqrt{2}$ | D. | 8+2$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com