
|
|
|
| n2+6n |
| 4 |
| 2n+2-4 |
| 3 |
| n2+8n+7 |
| 4 |
| 2n+1-4 |
| 3 |


科目:高中数学 来源: 题型:
 学校为了调查学生在课外读物方面的支出情况,将支出分区间[20,30)、[30,40)、[40,50)、[50,60)进行统计,现抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出在[50,60)元的同学有24人,则n的值为( )
学校为了调查学生在课外读物方面的支出情况,将支出分区间[20,30)、[30,40)、[40,50)、[50,60)进行统计,现抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出在[50,60)元的同学有24人,则n的值为( )| A、80 | B、800 |
| C、72 | D、720 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| m | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
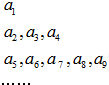 将数列{an}中的所有项按每一行比上一行多两项的规则排列成如图数表,已知图中的第一列数a1,a2,a5…构成一个等差数列,记为数列{bn},且b2=4,b5=10,图中每一行正中间一个数a1,a3,a7…构成数列{cn},其前n项和为Sn.
将数列{an}中的所有项按每一行比上一行多两项的规则排列成如图数表,已知图中的第一列数a1,a2,a5…构成一个等差数列,记为数列{bn},且b2=4,b5=10,图中每一行正中间一个数a1,a3,a7…构成数列{cn},其前n项和为Sn.| 5 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| α+β |
| x+y |
| α |
| x |
| β |
| y |
| 1 |
| 4 |
| α |
| x |
| β |
| y |
查看答案和解析>>
科目:高中数学 来源: 题型:
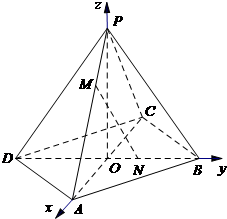 如图,在空间直角坐标系O-xyz中,正四棱锥P-ABCD的侧棱长与底边长都为3
如图,在空间直角坐标系O-xyz中,正四棱锥P-ABCD的侧棱长与底边长都为3| 2 |
| PM |
| PA |
| BN |
| BD |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com