
 如图,在三棱锥P-ABC中,△PAB和△CAB都是以AB为斜边的等腰直角三角形,若AB=2PC=$\sqrt{2}$,D是PC的中点
如图,在三棱锥P-ABC中,△PAB和△CAB都是以AB为斜边的等腰直角三角形,若AB=2PC=$\sqrt{2}$,D是PC的中点分析 (1)利用直线平面的垂直来证明得出AB⊥平面PEC,再利用转为直线直线的垂直证明.
(2)作出AD与平面ABC所成角的角,转化为三角形求解即可.
解答 证明:(1)取AB中点E,
∵△PAB和△CAB都是以AB为斜边的等腰直角三角形
∴CE⊥AB,PE⊥AB,
∵CE∩PE=E,
∴∵PC?平面PEC
∴AB⊥PC
解:(2)∵$PE=CE=\frac{{\sqrt{2}}}{2}$,
∴角形PEC为正三角形,
过P作PO⊥CE,则PO⊥平面ABC,
过D作DH平行PO,则DH⊥平面ABC,
连AH,则∠DAH为所求角
$PO=\frac{{\sqrt{6}}}{4}$,$DH=\frac{{\sqrt{6}}}{8},AD=\frac{{\sqrt{14}}}{4}$,$sin∠DAH=\frac{DH}{AD}=\frac{{\sqrt{21}}}{14}$.
点评 本题考查了直线平面的垂直问题,空间平面的转化思想,分析问题的能力,属于中档题,但是难度不大.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:解答题
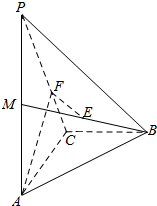 如图,在四面体P-ABC中,PA⊥面ACB,BC⊥AC,M是PA的中点,E是BM的中点,AC=2,PA=4,F是线段PC上的点,且EF∥面ACB.
如图,在四面体P-ABC中,PA⊥面ACB,BC⊥AC,M是PA的中点,E是BM的中点,AC=2,PA=4,F是线段PC上的点,且EF∥面ACB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30米,并在C测得塔顶A的仰角为60°,则塔的高度AB为( )
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30米,并在C测得塔顶A的仰角为60°,则塔的高度AB为( )| A. | 15$\sqrt{2}$米 | B. | 15$\sqrt{3}$米 | C. | 15($\sqrt{3}$+1)米 | D. | 15$\sqrt{6}$米 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| PM 2.5日均值(微克/立方米) | [25,35] | (35,45] | (45,55] | (55,65] | (65,75] | (75,85] |
| 频数 | 3 | 1 | 1 | 1 | 1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
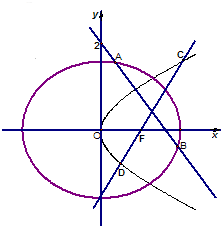 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率为$\frac{1}{2}$,椭圆C的右焦点F和抛物线G:y2=4x的焦点相同.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率为$\frac{1}{2}$,椭圆C的右焦点F和抛物线G:y2=4x的焦点相同.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在正方体ABCD一A1B1C1D1中,AB=3,CE=2EC1.
如图,在正方体ABCD一A1B1C1D1中,AB=3,CE=2EC1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com