
分析 (1)分别由等比数列的通项公式和求和公式计算两边的式子,验证可得;
(2)由(1)和对数的运算可得log2an=-n,可得bn=-(1+2+3+…+n),由等差数列的求和公式可得.
解答 (1)证明:∵等比数列{an}中,a1=$\frac{1}{2}$,公比q=$\frac{1}{2}$,
∴Sn=$\frac{\frac{1}{2}[1-(\frac{1}{2})^{n}]}{1-\frac{1}{2}}$=1-($\frac{1}{2}$)n,1-an=1-$\frac{1}{2}$($\frac{1}{2}$)n-1=1-($\frac{1}{2}$)n,
∴Sn=1-an;
(2)解:由(1)可知an=($\frac{1}{2}$)n,故log2an=-n,
∴bn=log2a1+log2a2+…+log2an=-1+(-2)+(-3)+…+(-n)
=-(1+2+3+…+n)=-$\frac{n(1+n)}{2}$.
点评 本题考查等比数列的通项公式和求和公式,涉及等差数列的求和公式,属基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | (-2,0) | B. | (-∞,-2)∪(1,+∞) | C. | (-2,1) | D. | (-∞,-4)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 任意实数 | B. | 负实数 | C. | 0<x≤$\frac{1}{2}$ | D. | 0≤x≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
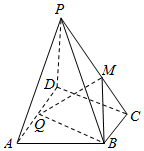 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,PD⊥底面ABCD,∠ADC=90°,AD=2BC,Q为AD的中点,M为棱PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,PD⊥底面ABCD,∠ADC=90°,AD=2BC,Q为AD的中点,M为棱PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,f(x)=0且g(x)=0 | B. | ?x∈R,f(x)=0或g(x)=0 | ||
| C. | ?x0∈R,f(x0)=0且g(x0)=0 | D. | ?x0∈R,f(x0)=0或g(x0)=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com