
分析 利用排列的定义,即可得出结论.
解答 解:(1)会场有50个座位,要求选出3个座位有多少种方法,与顺序无关,不是排列问题,
若选出3个座位安排三位客人,又有多少种方法?与顺序有关,是排列问题;
(2)任取两个元素作为a,b,可以得到多少个焦点在x轴上的椭圆方程$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1?可以得到多少个焦点在x轴上的双曲线方程$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1?
都与顺序有关,属于排列问题
点评 本题考查排列的定义,考查学生对概念的理解,比较基础.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
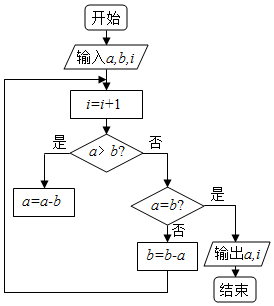 如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为12,16,0,则输出a和i的值分别为( )
如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为12,16,0,则输出a和i的值分别为( )| A. | 4,3 | B. | 4,4 | C. | 4,5 | D. | 3,4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
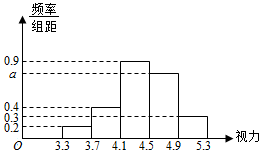 某市教育主管部门为调查该市高三学生的视力情况,从全市随机抽取了100名学生迸行检测,并将视力以[3.3,3.7),[3.7,4.1),[4.1,4.5),[4.5,4.9),[4.9,5.3]分段进行统计,得到如图所示的频率分布直方图.
某市教育主管部门为调查该市高三学生的视力情况,从全市随机抽取了100名学生迸行检测,并将视力以[3.3,3.7),[3.7,4.1),[4.1,4.5),[4.5,4.9),[4.9,5.3]分段进行统计,得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
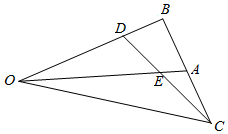 如图:已知,在△OAB中,点A是BC的中点,点D是将向量$\overrightarrow{OB}$分为2:1的一个分点,DC和OA交于点E,则AO与OE的比值是( )
如图:已知,在△OAB中,点A是BC的中点,点D是将向量$\overrightarrow{OB}$分为2:1的一个分点,DC和OA交于点E,则AO与OE的比值是( )| A. | 2 | B. | $\frac{5}{4}$ | C. | $\frac{3}{2}$ | D. | $\frac{6}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com