考点:棱柱、棱锥、棱台的体积,与二面角有关的立体几何综合题
专题:空间位置关系与距离
分析:(1)由正方体的性质证出AE⊥A1E,AE⊥A1D1,由线面垂直的判定证明AE⊥平面A1D1E;
(2)取AA1的中点O,过O在平面ADD1A1中作OF⊥AD1,交AD1于F、连EF,根据二面角的定义证明∠EFO为二面角E-AD1-A1的平面角,在△AFO中求解即可;
(3)由(2)中的结论将点E到面AD1C1的距离,转化为点F到面AD1C1的距离,再换底后代入三棱锥的体积公式求值.
解答:
证明:(1)由正方体的性质得,A
1D
1⊥面A
1B
1BA,
∴AE⊥A
1D
1,
∵AB=AD=1,BB
1=2,E为BB
1的中点,∴AE⊥A
1E,
又A
1E∩A
1D
1=A
1,∴AE⊥平面A
1D
1E.
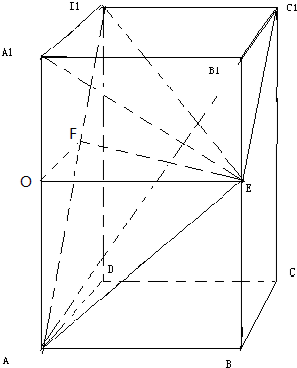
解:(2)取AA
1的中点O,连OE,
则EO⊥AA
1、EO⊥A
1D
1,
AA
1∩A
1D
1=A
1,
∴EO⊥平面ADD
1A
1,∴EO⊥AD
1,
过O在平面ADD
1A
1中作OF⊥AD
1,交AD
1于F,
连EF,则AD
1⊥面EFO,
∴AD
1⊥EF,
∴∠EFO为二面角E-AD
1-A
1的平面角.
在△AFO中,
OF=OA•sin∠OAF=OA•=
1×=
.
则
tan∠EFO=.
(3)由(2)知,EO∥D
1C
1,
且EO?面AD
1C
1,D
1C
1?面AD
1C
1,
∴EO∥面AD
1C
1,
又∵OF⊥AD
1,OF⊥D
1C
1,
∴OF⊥面AD
1C
1,
则点E到面AD
1C
1的距离是点F到面AD
1C
1的距离,
∴
VA-C1D1E=
VE-AC1D1=
•S△AC1D1•OF=
××1××=
.
点评:本题考查了二面角的求解过程,换底求三棱锥的体积,线面垂直的定义,性质、判定,考查了空间想象能力、计算能力,分析解决问题能力,空间问题平面化是解决空间几何体问题最主要的思想方法.

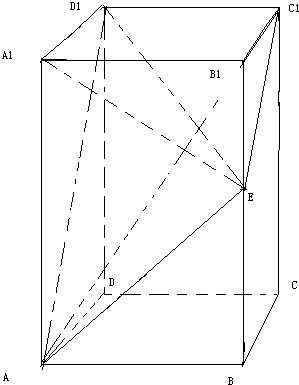 长方体ABCD-A1B1C1D1中,AB=AD=1,BB1=2,E为BB1的中点.(1)求证:AE⊥平面A1D1E;
长方体ABCD-A1B1C1D1中,AB=AD=1,BB1=2,E为BB1的中点.(1)求证:AE⊥平面A1D1E; AA1∩A1D1=A1,
AA1∩A1D1=A1,

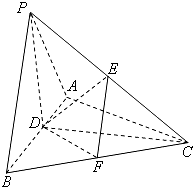 如图,在三棱锥P-ABC中,△PAB是等边三角形,D、E分别为AB、PC的中点.
如图,在三棱锥P-ABC中,△PAB是等边三角形,D、E分别为AB、PC的中点.