
���� ��1��������ֵ�ɵ�a=$\frac{1}{100}$���������ʽ���ɣ�
��2���������������������õ����������ĵ����ԣ����������������ֵ��
��� �⣺��1���ߵ�x=10ʱ��y=$\frac{22}{5}$����$\frac{27}{50}$��10-a��102-ln 1=$\frac{22}{5}$�����a=$\frac{1}{100}$��
��f��x��=$\frac{27}{50}$x-$\frac{x2}{100}$-ln $\frac{x}{10}$��x�ʣ�2��t]����4�֣�
��2����f��x������$f'��x��=\frac{27}{50}-\frac{x}{50}-\frac{1}{x}=-\frac{{{x^2}-27x+50}}{50x}=-\frac{��x-2����x-25��}{50x}$��
��f�䣨x��=0����x=25��x=2����ȥ��������6�֣�
��x�ʣ�2��25��ʱ��f�䣨x����0��
��f��x���ڣ�2��25��������������
��x�ʣ�25��+�ޣ�ʱ��f�䣨x����0��
��f��x���ڣ�25��+�ޣ����Ǽ�����
���Ե�t��25ʱ����x�ʣ�2��25��ʱ��f�䣨x����0��f��x���ڣ�2��25��������������
��x�ʣ�25��t]ʱ��f�䣨x����0��f��x���ڣ�25��t]���Ǽ�������
�൱x=25ʱ��yȡ�����ֵ�� ����8�֣�
��2��t��25ʱ����x�ʣ�2��t��ʱ��f�䣨x����0��f��x���ڣ�2��t��������������
�൱x=tʱ��yȡ�����ֵ ����10�֣�
���ϣ���t��25ʱ��x=25ʱ��yȡ�����ֵ
��2��t��25ʱ��x=tʱ��yȡ�����ֵ����12�֣�
���� �����˺�����Ӧ�ú͵�������������ֵ���ѵ��Ƕ��Ա���t��ȡֵ�������ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}\overrightarrow{a}+\frac{2}{3}\overrightarrow{b}$ | B�� | $\frac{2}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}$ | C�� | $\frac{3}{5}\overrightarrow{a}+\frac{4}{5}\overrightarrow{b}$ | D�� | $\frac{4}{5}\overrightarrow{a}+\frac{3}{5}\overrightarrow{b}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
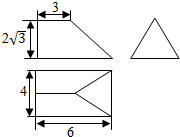
| A�� | 12$\sqrt{3}$ | B�� | 16$\sqrt{3}$ | C�� | 20$\sqrt{3}$ | D�� | 32$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����ƽ��$\frac{��}{6}$����λ | B�� | ����ƽ��$\frac{��}{3}$����λ | ||
| C�� | ����ƽ��$\frac{2��}{3}$����λ | D�� | ����ƽ��$\frac{2��}{3}$����λ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
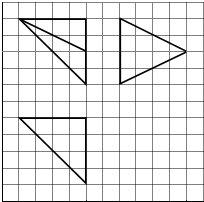 ��ͼ������ֽ��С�����εı߳�Ϊ1����ʵ��������ij�����������ͼ����ö�����ĸ������У�ֱ�������εĸ����ǣ�������
��ͼ������ֽ��С�����εı߳�Ϊ1����ʵ��������ij�����������ͼ����ö�����ĸ������У�ֱ�������εĸ����ǣ�������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com