
【题目】某单位科技活动纪念章的结构如图所示,O是半径分别为1cm,2cm的两个同心圆的圆心,等腰△ABC的顶点A在外圆上,底边BC的两个端点都在内圆上,点O,A在直线BC的同侧.若线段BC与劣弧![]() 所围成的弓形面积为S1,△OAB与△OAC的面积之和为S2, 设∠BOC=2
所围成的弓形面积为S1,△OAB与△OAC的面积之和为S2, 设∠BOC=2![]() .
.

(1)当![]() 时,求S2﹣S1的值;
时,求S2﹣S1的值;
(2)经研究发现当S2﹣S1的值最大时,纪念章最美观,求当纪念章最美观时,cos![]() 的值.(求导参考公式:(sin2x)'=2cos2x,(cos2x)'=﹣2sin2x)
的值.(求导参考公式:(sin2x)'=2cos2x,(cos2x)'=﹣2sin2x)
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两个班级(各40名学生)进行一门考试,为易于统计分析,将甲、乙两个班学生的成绩分成如下四组:![]() ,
,![]() ,
,![]() ,
,![]() ,并分别绘制了如下的频率分布直方图:
,并分别绘制了如下的频率分布直方图:
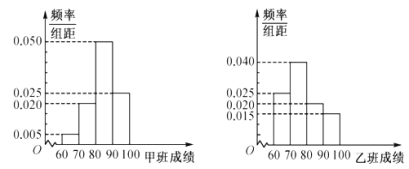
规定:成绩不低于90分的为优秀,低于90分的为不优秀.
(1)根据这次抽查的数据,填写下面的![]() 列联表:
列联表:
优秀 | 不优秀 | 合计 | |
甲班 | |||
乙班 | |||
合计 |
(2)根据(1)中的列联表,能否有![]() 的把握认为成绩是否优秀与班级有关?
的把握认为成绩是否优秀与班级有关?
附:临界值参考表与参考公式
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(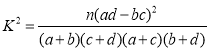 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,过点![]() 的直线l与抛物线
的直线l与抛物线![]() 交于A,B两点,以AB为直径作圆,记为
交于A,B两点,以AB为直径作圆,记为![]() ,
,![]() 与抛物线C的准线始终相切.
与抛物线C的准线始终相切.
(1)求抛物线C的方程;
(2)过圆心M作x轴垂线与抛物线相交于点N,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三年级为了解学生在家参加线上教学的学习情况,对高三年级进行了网上数学测试,他们的成绩在80分到150分之间,根据统计数据得到如下频率分布直方图:
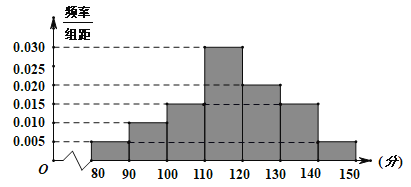
若成绩在区![]() 左侧,认为该学生属于“网课潜能生”,成绩在区间
左侧,认为该学生属于“网课潜能生”,成绩在区间![]() 之间,认为该学生属于“网课中等生”,成绩在区间
之间,认为该学生属于“网课中等生”,成绩在区间![]() 右侧,认为该学生属于“网课优等生”.
右侧,认为该学生属于“网课优等生”.
(1)若小明的测试成绩为100分,请判断小明是否属于“网课潜能生”,并说明理由:(参考数据:计算得![]() )
)
(2)该校利用分层抽样的方法从样本的![]() ,
,![]() 两组中抽出6人,进行教学反馈,并从这6人中再抽取2人,赠送一份学习资料,求获赠学习资料的2人中恰有1人成绩超过90分的概率.
两组中抽出6人,进行教学反馈,并从这6人中再抽取2人,赠送一份学习资料,求获赠学习资料的2人中恰有1人成绩超过90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点到直线
的焦点到直线![]() 的距离为
的距离为![]() ,过点
,过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求抛物线![]() 的准线方程;
的准线方程;
(2)设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,若
,若![]() ,且
,且![]() 与
与![]() 的交点在抛物线
的交点在抛物线![]() 上,求直线
上,求直线![]() 的斜率和点
的斜率和点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() 的焦点为
的焦点为![]() ,准线与
,准线与![]() 轴的交点为
轴的交点为![]() .过点
.过点![]() 的直线与抛物线相交于
的直线与抛物线相交于![]() 、
、![]() 两点,
两点,![]() 、
、![]() 分别与
分别与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,当
两点,当![]() 轴时,
轴时,![]() .
.
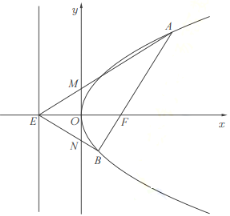
(1)求抛物线的方程;
(2)设![]() 的面积为
的面积为![]() ,
,![]() 面积为
面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() ,
,![]() 分别是其左、右焦点,过
分别是其左、右焦点,过![]() 的直线l与椭圆C交于A,B两点,且椭圆C的离心率为
的直线l与椭圆C交于A,B两点,且椭圆C的离心率为![]() ,
,![]() 的内切圆面积为
的内切圆面积为![]() ,
,![]() .
.
(I)求椭圆C的方程;
(II)若![]() 时,求直线l的方程
时,求直线l的方程
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率与双曲线
的离心率与双曲线![]() 的离心率互为倒数,
的离心率互为倒数,![]() 分别为椭圆的左、右顶点,且
分别为椭圆的左、右顶点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知过左顶点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 另交于点
另交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,在平面内是否存在一定点
,在平面内是否存在一定点![]() ,使得
,使得![]() 恒成立?若存在,求出该点的坐标,并求
恒成立?若存在,求出该点的坐标,并求![]() 面积的最大值;若不存在,说明理由.
面积的最大值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com