
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{5}}{3}$ | C. | $\frac{\sqrt{10}}{4}$ | D. | $\frac{\sqrt{17}}{5}$ |
分析 取AB中点H,椭圆另一个焦点为E,连结PE根据平面几何的知识、勾股定理及中位线的性质得a=5d
解答 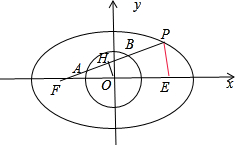 解:如图,取AB中点H,椭圆另一个焦点为E,连结PE.
解:如图,取AB中点H,椭圆另一个焦点为E,连结PE.
∵A、B三等分线段PF,∴H也是AB中点,即OH⊥AB
设OH=d,则PE=2d,PF=2a-2d,AH=$\frac{a-d}{3}$,
在Rt△OHA中,OA2=OH2+AH2,解得a=5d.
在Rt△OHF中,FH=$\frac{4}{5}a$,OH=$\frac{a}{5}$,OF=c,由OF2=OH2+FH2
化简得17a2=25c2,$\frac{c}{a}=\frac{\sqrt{17}}{5}$.即C的离心率为$\frac{\sqrt{17}}{5}$.
故选:D.
点评 本题考查椭圆离心率的求解问题,关键是根据题设条件获得关于a,b,c的关系式,最后化归为a,c(或e)的关系式,利用方程求解.属于中档题.


科目:高中数学 来源: 题型:填空题
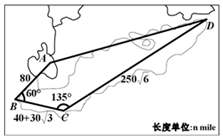 某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,$BC=40+30\sqrt{3}$nmile,$CD=250\sqrt{6}$nmile.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,则收到指令时该轮船到城市C的距离是100nmile.
某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,$BC=40+30\sqrt{3}$nmile,$CD=250\sqrt{6}$nmile.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,则收到指令时该轮船到城市C的距离是100nmile.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
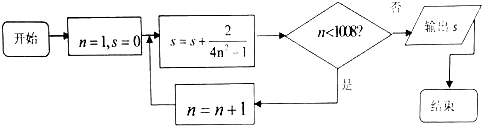
| A. | 1 | B. | $\frac{2018}{2019}$ | C. | $\frac{2018}{2017}$ | D. | $\frac{2016}{2017}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{8}$ | B. | $\frac{1}{8}$ | C. | $-\frac{1}{6}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com