
分析 由条件$|\overrightarrow{a}-\overrightarrow{b}{|}^{2}=4$,进行数乘的运算便可得到$|\overrightarrow{a}{|}^{2}+|\overrightarrow{b}{|}^{2}=8$,从而可设$|\overrightarrow{a}|=2\sqrt{2}cosθ,|\overrightarrow{b}|=2\sqrt{2}sinθ$,这样便可得出S△AOB=2sin2θsin∠AOB,从而sin2θ=1时△AOB的面积最大,这样由$\overrightarrow{a}•\overrightarrow{b}=2$即可得到$cos∠AOB=\frac{1}{2}$,从而便可得出∠AOB的大小.
解答 解:根据条件$|\overrightarrow{a}-\overrightarrow{b}{|}^{2}=|\overrightarrow{a}{|}^{2}-4+|\overrightarrow{b}{|}^{2}=4$;
∴$|\overrightarrow{a}{|}^{2}+|\overrightarrow{b}{|}^{2}=8$;
∴设$|\overrightarrow{a}|=2\sqrt{2}cosθ,|\overrightarrow{b}|=2\sqrt{2}sinθ$;
∴${S}_{△AOB}=\frac{1}{2}|\overrightarrow{a}||\overrightarrow{b}|sin∠AOB$=2sin2θsin∠AOB;
∴sin2θ=1时,△AOB的面积最大;
∴此时,$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos∠AOB=4sin2θcos∠AOB=4cos∠AOB=2$;
∴$cos∠AOB=\frac{1}{2}$;
∴$∠AOB=\frac{π}{3}$.
点评 考查向量数量积的运算及其计算公式,cos2x+sin2x=1,圆的参数方程,三角形的面积公式:$S=\frac{1}{2}absinC$,以及正弦函数的最值.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1} | B. | {1} | C. | {-1,1} | D. | {0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | (0,1) | C. | [0,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
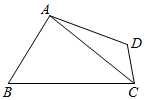 如图,在四边形ABCD中,∠ABC=$\frac{π}{3}$,AB:BC=2:3,$AC=\sqrt{7}$.
如图,在四边形ABCD中,∠ABC=$\frac{π}{3}$,AB:BC=2:3,$AC=\sqrt{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| X | 0.52 | 0.36 | 0.58 | 0.73 | 0.41 | 0.6 | 0.05 | 0.32 | 0.38 | 0.73 |
| Y | 0.76 | 0.39 | 0.37 | 0.01 | 0.04 | 0.28 | 0.03 | 0.15 | 0.14 | 0.86 |
| 组别 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| X | 0.67 | 0.47 | 0.58 | 0.21 | 0.54 | 0.64 | 0.36 | 0.35 | 0.95 | 0.14 |
| Y | 0.41 | 0.54 | 0.51 | 0.37 | 0.31 | 0.23 | 0.56 | 0.89 | 0.17 | 0.03 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 不存在这样的三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com