
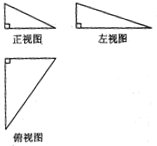
 一个三棱锥的三视图如图所示,其正视图、左视图、俯视图的面积分别是1,2,4,则这个几何体的外接球的表面积为21π.
一个三棱锥的三视图如图所示,其正视图、左视图、俯视图的面积分别是1,2,4,则这个几何体的外接球的表面积为21π. 分析 几何体是一个三棱锥,一条侧棱与底面垂直,底面是一个直角三角形,根据正视图、侧视图、俯视图面积分别是1、2、4.求出三条边的长度,这个三棱锥的外接球也是以这个三棱锥三条侧棱为棱的长方体的外接球,做出长方体的直径,求出球的表面积.
解答 解:由题意知几何体是一个三棱锥,一条侧棱与底面垂直,底面是一个直角三角形,
∵正视图、侧视图、俯视图面积分别是1、2、4,
设出三条互相垂直的棱长是x,y,z,
有xz=2,yz=4,xy=8,
∴x=2,y=4,z=1,
这个三棱锥的外接球也是以这个三棱锥三条侧棱为棱的长方体的外接球,
长方体的直径是2R=$\sqrt{4+16+1}$=$\sqrt{21}$,
∴几何体的外接球的表面积是4π×$\frac{21}{4}$=21π,
故答案为:21π.
点评 本题考查球和几何体之间的关系,本题解题的关键是根据三条侧棱两两垂直的关系得到由这三条侧棱构成的长方体,从而得到外接球的表面积.


 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\sqrt{3}$ | B. | $\frac{{1+\sqrt{3}}}{2}$ | C. | $\sqrt{13}$ | D. | $\frac{{1+\sqrt{13}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -sin4x | B. | cos4x | C. | sinx | D. | -cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图:在三棱锥P-ABC中,AB=AC=2$\sqrt{10}$,BC=4,PC=2$\sqrt{11}$,点P在平面ABC内的射影恰为△ABC的重心G,M为侧棱AP上一动点.
如图:在三棱锥P-ABC中,AB=AC=2$\sqrt{10}$,BC=4,PC=2$\sqrt{11}$,点P在平面ABC内的射影恰为△ABC的重心G,M为侧棱AP上一动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 1 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥1 | B. | a≤1 | C. | a≥-1 | D. | a≤-3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com