
分析 可画出图形,进行数量积的运算便可由$\overrightarrow{AB}•\overrightarrow{AC}=\overrightarrow{BA}•\overrightarrow{BC}=2$得到bccosA=accosB=2,由正弦定理即可得出A=B,进而得到a=b,然后由余弦定理,根据bccosA=2即可求出c的值.
解答 解:如图,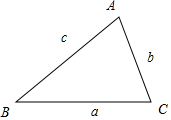
∵$\overrightarrow{AB}•\overrightarrow{AC}=\overrightarrow{BA}•\overrightarrow{BC}=2$;
∴bccosA=accosB=2;
∴bcosA=acosB;
根据正弦定理,b=2RsinB,a=2RsinA,代入上式:2RsinBcosA=2RcosBsinA;
∴sinBcosA=cosBsinA;
∴sin(B-A)=0;
∵A,B∈(0,π);
∴A=B;
∴a=b
由余弦定理,$cosA=\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{c}{2b}$,代入bccosA=2得:$bc•\frac{c}{2b}=2$;
∴c2=4;
∴c=2.
故答案为:2.
点评 考查了数量积的计算公式,以及正余弦定理,等腰三角形的概念.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,3) | B. | (1,3] | C. | (1,3) | D. | [3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{{{(x+1)}^2}}}{4}-\frac{{{{(y+2)}^2}}}{9}=1$ | B. | $\frac{{{{(x-1)}^2}}}{4}-\frac{{{{(y-2)}^2}}}{9}=1$ | C. | $\frac{{{{(x+1)}^2}}}{4}+\frac{{{{(y+2)}^2}}}{9}=1$ | D. | $\frac{{{{(x-1)}^2}}}{4}+\frac{{{{(y-2)}^2}}}{9}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| PM2.5日均值k(微克) | 空气质量等级 |
| k≤35 | 一级 |
| 35<k<75 | 二级 |
| k>75 | 超标 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30种 | B. | 36种 | C. | 42种 | D. | 48种 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
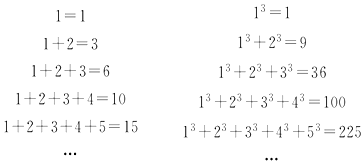
| A. | $\frac{1}{4}{n^2}{(n-1)^2}$ | B. | $\frac{1}{4}{n^2}{(n-2)^2}$ | C. | $\frac{1}{4}{n^2}{(n+1)^2}$ | D. | $\frac{1}{4}{n^2}{(n+2)^2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com