
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 斜三角形 |
分析 根据正弦定理结合题中的等式,化简得sinCcosA=sinB,再用sin(A+C)=sinB展开化简得到cosCsinA=0,结合三角形内角的范围即可得到C=$\frac{π}{2}$,即△ABC是直角三角形.
解答 解:∵在△ABC中,ccosA=b,
∴根据正弦定理,得sinCcosA=sinB,…①
∵A+C=π-B,
∴sin(A+C)=sinB,即sinB=sinCcosA+cosCsinA,
将①代入,可得cosCsinA=0,
∵A、C∈(0,π),可得sinA>0,
∴cosC=0,得C=$\frac{π}{2}$,即△ABC是直角三角形,
故选:C.
点评 本题给出三角形的边角关系,判断三角形的形状,着重考查了两角和的正弦公式和正弦定理等知识,属于基础题.


 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 16 | C. | 12 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
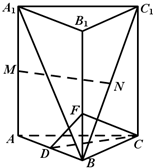 如图所示,在直三棱柱ABC-A1B1C1中,D、M、N分别是AB、AA1、BC1的中点.
如图所示,在直三棱柱ABC-A1B1C1中,D、M、N分别是AB、AA1、BC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com