
【题目】(导学号:05856325)已知函数f(x)=![]() +eln x,直线l:y=kx(k≠0)与函数f(x)的图象相切于点A(t,f(t))(f(t)≠0),则( )
+eln x,直线l:y=kx(k≠0)与函数f(x)的图象相切于点A(t,f(t))(f(t)≠0),则( )
A. t∈(0,1) B. t∈(1,e) C. t∈(e,3) D. t∈(3,e2)
【答案】B
【解析】由题可得f′(x)=-![]() +
+![]() ,故k=-
,故k=-![]() +
+![]() ,∴直线l的方程可转化为y=(-
,∴直线l的方程可转化为y=(-![]() +
+![]() )x,又∵A在函数f(x)的图象上,
)x,又∵A在函数f(x)的图象上,
结合y=(-![]() +
+![]() )x可得,
)x可得,
实数t必满足方程![]() +eln t-e=0,令g(t)=
+eln t-e=0,令g(t)=![]() +eln t-e,则g′(t)=-
+eln t-e,则g′(t)=-![]() +
+![]() =
=![]() ,
,
解g′(t)>0得t>![]() ,g′(t)<0得0<t<
,g′(t)<0得0<t<![]() ,∴函数y=g(t)在(0,
,∴函数y=g(t)在(0, ![]() ]上递减,在(
]上递减,在(![]() ,+∞)上递增,∵g(
,+∞)上递增,∵g(![]() )=0,且函数y=g(t)在(0,
)=0,且函数y=g(t)在(0, ![]() )上递减,
)上递减,
∴t=![]() 是方程
是方程![]() +eln t-e=0在区间(0,
+eln t-e=0在区间(0, ![]() ]内的唯一一个解,又∵f(
]内的唯一一个解,又∵f(![]() )=0,∴t=
)=0,∴t=![]() 不合题意,即t>
不合题意,即t>![]() .∵g(1)=2-e<0,g(e)=
.∵g(1)=2-e<0,g(e)=![]() >0,函数y=g(t)在(
>0,函数y=g(t)在(![]() ,+∞)上递增,∴ 必有1<t<e.
,+∞)上递增,∴ 必有1<t<e.
故选:B


科目:高中数学 来源: 题型:
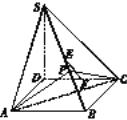
【题目】四棱锥S-ABCD中的底面是菱形,∠BAD=60°,SD⊥底面ABCD,SD=AB=2,E、F分别为SB、CD的中点.
(Ⅰ)求证:EF∥平面SAD;
(Ⅱ)点P是SB上一点,若SB⊥平面APC,试确定点P的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856306)
在△ABC中,内角A,B,C的对边分别为a,b,c,已知![]() ,且b=5,acos C=-1.
,且b=5,acos C=-1.
(Ⅰ)求角A;
(Ⅱ)求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为______元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856334)
已知函数f(x)=ln x+ax2+1.
(Ⅰ)当a=-1时,求函数f(x)的极值;
(Ⅱ)当a>0时,证明:存在正实数λ,使得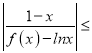 λ恒成立.
λ恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线C:
为抛物线C:![]() 的焦点,过点
的焦点,过点![]() 的动直线
的动直线![]() 与抛物线C交于
与抛物线C交于![]() ,
,![]() 两点,如图.当直线
两点,如图.当直线![]() 与
与![]() 轴垂直时,
轴垂直时,![]() .
.
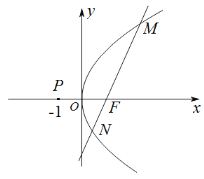
(1)求抛物线C的方程;
(2)已知点![]() ,设直线PM的斜率为
,设直线PM的斜率为![]() ,直线PN的斜率为
,直线PN的斜率为![]() .请判断
.请判断![]() 是否为定值,若是,写出这个定值,并证明你的结论;若不是,说明理由.
是否为定值,若是,写出这个定值,并证明你的结论;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型娱乐场有两种型号的水上摩托,管理人员为了了解水上摩托的使用及给娱乐城带来的经济收入情况,对该场所最近6年水上摩托的使用情况进行了统计,得到相关数据如表:
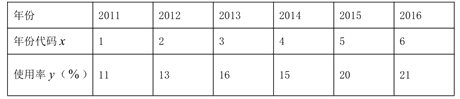
(1)请根据以上数据,用最小二乘法求水上摩托使用率![]() 关于年份代码
关于年份代码![]() 的线性回归方程,并预测该娱乐场2018年水上摩托的使用率;
的线性回归方程,并预测该娱乐场2018年水上摩托的使用率;
(2)随着生活水平的提高,外出旅游的老百姓越来越多,该娱乐场根据自身的发展需要,准备重新购进一批水上摩托,其型号主要是目前使用的Ⅰ型、Ⅱ型两种,每辆价格分别为1万元、1.2万元.根据以往经验,每辆水上摩托的使用年限不超过四年.娱乐场管理部对已经淘汰的两款水上摩托的使用情况分别抽取了50辆进行统计,使用年限如条形图所示:

已知每辆水上摩托从购入到淘汰平均年收益是0.8万元,若用频率作为概率,以每辆水上摩托纯利润(纯利润=收益-购车成本)的期望值为参考值,则该娱乐场的负责人应该选购Ⅰ型水上摩托还是Ⅱ型水上摩托?
附:回归直线方程为![]() ,其中
,其中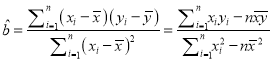 ,
, ![]() .参考数据
.参考数据![]() ,
, ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com