
| A. | $\frac{6}{5}$ | B. | $\frac{7}{5}$ | C. | $\frac{5}{8}$ | D. | $\frac{9}{5}$ |
分析 设AF=4m,BF=m.过A,B分别做准线的垂线,垂足为A1,B1.由双曲线定义得可分别表示出|AA1|和|BB1|,过B做BD垂直于AA1垂足D.根据直线的斜率可知∠ABD=30°进而求得|AD|和|AB|的关系求得e.
解答 解:设|AF|=4m,|BF|=m.
过A,B分别做准线的垂线,垂足为A1,B1.
由双曲线的第二定义得,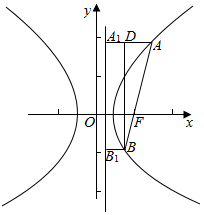
|AA1|=$\frac{4m}{e}$.|BB1|=$\frac{m}{e}$.过B做BD垂直于AA1垂足D.
在△ABD中,∠ABD=30°,|AD|=$\frac{1}{2}$|AB|.
即$\frac{3m}{e}$=$\frac{1}{2}$×5m.
解得e=$\frac{6}{5}$.
故选:A.
点评 本题主要考查了直线与圆锥曲线的综合问题,考查双曲线的离心率的求法,注意运用定义法,考查了学生综合分析问题和解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 公平 | B. | 企业A吃亏 | C. | 个人B吃亏 | D. | 谁吃亏与a有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | [2$\sqrt{2}$,+∞) | C. | [2$\sqrt{3}$,+∞) | D. | [4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,1] | B. | $[-3,\frac{3}{2}]$ | C. | $[-1,\frac{3}{2}]$ | D. | [-1,1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com