考点:函数恒成立问题,函数单调性的判断与证明,函数奇偶性的判断
专题:函数的性质及应用
分析:(1)设x
1,x
2∈R,且x
1<x
2,由定义法能推导出f(x
1)-f(x
2)<0,从而得到不论a为何实数,f(x)在定义域上单调递增.
(2)由f(-x)=-f(x),得
a-=a-,由此能示出a.
(3)由条件可得m≤2
x(1-
)=(2
x+1)+
-3恒成立,从而m≤(2
x+1)+
-3的最小值,x∈[2,3],由此能求出m的最大值.
解答:
解:(1)不论a为何实数,f(x)在定义域上单调递增.
证明:设x
1,x
2∈R,且x
1<x
2,
则
f(x1)-f(x2)=(a-)-(a-)=
,
由x
1<x
2,知0<
2x1<2x2,
∴
2x1-2x20,
2x2+1>0,
∴f(x
1)-f(x
2)<0,
∴不论a为何实数,f(x)在定义域上单调递增.
(2)∵存在实数a使函数f(x)是奇函数,
∴由f(-x)=-f(x),得
a-=a-,
解得a=1.
(3)由条件可得m≤2
x(1-
)=(2
x+1)+
-3恒成立,
m≤(2
x+1)+
-3恒成立,
m≤(2
x+1)+
-3的最小值,x∈[2,3],
设t=2
x+1,则t∈[5,9],函数g(t)=t+
-3在[5,9]上单调递增,
∴g(t)的最小值是g(5)=
,m
≤,
∴m的最大值为
.
点评:本题考查函数f(x)的单调性的判断与证明,考查实数值的求法,考查使不等式恒成立的实数的最大值的求法,解题时要认真审题,注意函数性质的合理运用.



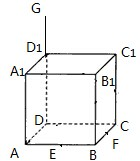 如图,G是正方体ABCD-A1B1C1D1的棱的DD1延长线上的一点,E、F是棱AB、BC的中点,试分别画出:
如图,G是正方体ABCD-A1B1C1D1的棱的DD1延长线上的一点,E、F是棱AB、BC的中点,试分别画出: