
| 1 |
| 1+x2 |
| a |
| 2 |
| 1 |
| 1+x2 |
| 1 |
| 1+(-x)2 |
| 1 |
| 1+x2 |
| 1 |
| 1+x12 |
| 1 |
| 1+x22 |
| (x2-x1)(x2+x1) |
| (x12+1)(x22+1) |
| a |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
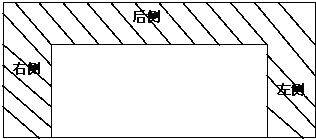 某村计划建造一个室内面积为72m2的矩形蔬菜温室.在温室内沿左、右两侧与后侧内墙各保留1m宽的通道,当矩形温室的边长各为多少时?蔬菜的种植面积最大,最大种植面积是多少?
某村计划建造一个室内面积为72m2的矩形蔬菜温室.在温室内沿左、右两侧与后侧内墙各保留1m宽的通道,当矩形温室的边长各为多少时?蔬菜的种植面积最大,最大种植面积是多少?查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 2x+1 |
| m |
| 2x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| -x2+5x-4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 4 |
| 1 |
| 2 |
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com