练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．已知曲线C1：$\left\{\begin{array}{l}x=12cosθ\\ y=4sinθ\end{array}\right.$（参数θ∈R），以坐标原点O为极点，x轴的非负半轴为极轴，建立极坐标系，曲线C2的极坐标方程为$ρ=\frac{3}{{cos（θ+\frac{π}{3}）}}$，点Q的极坐标为$（4\sqrt{2}，\frac{π}{4}）$．
    （1）将曲线C2的极坐标方程化为直角坐标方程，并求出点Q的直角坐标；
    （2）设P为曲线C1上的点，求PQ中点M到曲线C2上的点的距离的最小值．

    分析 （1）利用极坐标方程与直角坐标方程互化的方法，可得结论；
    （2）利用参数方程，结合三角函数知识，求PQ中点M到曲线C2上的点的距离的最小值．

    解答 解：（1）$ρ=\frac{3}{{cos（θ+\frac{π}{3}）}}$，得$\frac{1}{2}ρcosθ-\frac{{\sqrt{3}}}{2}ρsinθ=3$，
    故曲线C2的直角坐标方程为$x-\sqrt{3}y-6=0$，
    点Q的直角坐标为（4，4）．
    （2）设P（12cosθ，4sinθ），故PQ中点M（2+6cosθ，2+2sinθ），C2的直线方程为$x-\sqrt{3}y-6=0$，
    点M到C2的距离$d=\frac{{|2+6cosθ-\sqrt{3}（2+2sinθ）-6|}}{2}$=$|3cosθ-\sqrt{3}sinθ-2-\sqrt{3}|$
    =$|2\sqrt{3}cos（θ+\frac{π}{6}）-2-\sqrt{3}|≥|2\sqrt{3}-2-\sqrt{3}|=2-\sqrt{3}$，
    PQ中点M到曲线C2上的点的距离的最小值是$2-\sqrt{3}$．

    点评 本题考查极坐标方程与直角坐标方程互化，考查参数方程的运用，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    16．已知函数f（x）=$\frac{1}{a}$lnx+$\frac{1}{2}$x2-（1+$\frac{1}{a}$）x，其中a≠0．
    （1）求函数f（x）的单调区间；
    （2）证明：当n≥2时，$\frac{1}{3ln1+2}+\frac{1}{3ln2+2}+…+\frac{1}{3lnn+2}＞\frac{n}{n+1}$恒成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知$\overrightarrow{a}$=（3，-1），$\overrightarrow{a}$•$\overrightarrow{b}$=-5，$\overrightarrow{c}$=x$\overrightarrow{a}$+（1-x）$\overrightarrow{b}$．
    （Ⅰ）若$\overrightarrow{a}$⊥$\overrightarrow{c}$，求实数x的值；
    （Ⅱ）若|$\overrightarrow{b}$|=$\sqrt{5}$，求|$\overrightarrow{c}$|的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知函数$f（x）=4cosωxsin（{ωx-\frac{π}{6}}）（{ω＞0}）$的最小正周期是π．
    （1）求函数f（x）在区间x∈（0，π）的单调递增区间；
    （2）求f（x）在$[{\frac{π}{8}，\frac{3π}{8}}]$上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．执行如图所示的程序框图，如果输出T=6，那么判断框内应填入的条件是（　　）
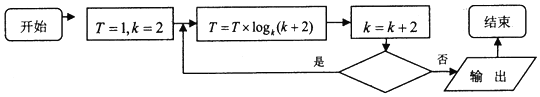
    A．k＜32B．k＜33C．k＜64D．k＜65

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．设F1，F2分别为椭圆C1：$\frac{x^2}{{{a_1}^2}}+\frac{y^2}{{{b_1}^2}}=1（{a_1}＞{b_1}＞0）$与双曲线C2：$\frac{x^2}{{{a_2}^2}}-\frac{y^2}{{{b_2}^2}}=1（{a_2}＞0，{b_2}＞0）$的公共焦点，它们在第一象限内交于点M，∠F1MF2=90°，若椭圆的离心率${e_1}=\frac{3}{4}$，则双曲线C2的离心率e2的值为（　　）
    A．$\frac{9}{2}$B．$\frac{{3\sqrt{2}}}{2}$C．$\frac{3}{2}$D．$\frac{5}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．在如图所示的程序图中，若函数f（x）=$\left\{\begin{array}{l}{{2}^{x}，αx≤0}\\{lo{g}_{\frac{1}{2}}x，x＞0}\end{array}\right.$，则输出的结果是（　　）
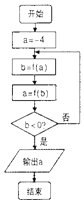
    A．-3B．$\frac{1}{16}$C．$\frac{1}{4}$D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知曲线C的参数方程是$\left\{\begin{array}{l}{x=2cosθ}\\{y=2sinθ}\end{array}\right.$（θ为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，A、B的极坐标分别为A-（2，0）、B（-1，$\sqrt{3}$）
    （1）求直线AB的直角坐标方程；
    （2）在曲线C上求一点M，使点M到AB的距离最大，并求出些最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．在单调递增的等比数列{an}中，a1•a9=64，a3+a7=20，求a11=64．

    查看答案和解析>>

    同步练习册答案