
| A. | a2+b2+c2≥2 | B. | (a+b+c)2≥3 | C. | $\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$≥2$\sqrt{3}$ | D. | abc(a+b+c)≥$\frac{1}{3}$ |
分析 根据不等式a2+b2≥2ab及条件便可判断出选项A错误,并且可得出a2+b2+c2≥1,进而可判断选项B正确;而由条件及三个正数的算术-几何平均不等式便可判断选项C错误;先得到abc(a+b+c)=(ab)(ca)+(ab)(bc)+(ca)(bc),由条件知1=(ab+bc+ca)2,这样由不等式a2+b2≥2ab便可说明选项D错误.
解答 解:A.∵$ab≤\frac{{a}^{2}+{b}^{2}}{2},bc≤\frac{{b}^{2}+{c}^{2}}{2},ca≤\frac{{c}^{2}+{a}^{2}}{2}$,且ab+bc+ca=1;
∴$\frac{{a}^{2}+{b}^{2}}{2}+\frac{{b}^{2}+{c}^{2}}{2}+\frac{{c}^{2}+{a}^{2}}{2}≥1$,当且仅当a=b=c=$\frac{\sqrt{3}}{3}$时取“=”;
即a2+b2+c2≥1,∴该选项错误;
B.根据上面得出的a2+b2+c2≥1,及ab+bc+ca=1得:
(a+b+c)2=a2+b2+c2+2(ab+bc+ca)
=a2+b2+c2+2
≥1+2=3;
∴该选项正确;
C.∵a,b,c∈R+;
∴由ab+bc+ca=1得,$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{abc}$;
∴$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}≥3\root{3}{\frac{1}{abc}}$=$3\root{3}{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}}$,当且仅当a=b=c=$\frac{\sqrt{3}}{3}$时取等号;
∴$(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})^{2}≥27$;
∴$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}≥3\sqrt{3}$,∴该选项错误;
D.abc(a+b+c)=(ab)(ca)+(ab)(bc)+(ca)(bc);
又1=(ab+bc+ca)2
=(ab)2+(bc)2+(ca)2+2[(ab)(bc)+(ab)(ca)+(bc)(ca)]
=$[\frac{(ab)^{2}}{2}+\frac{(bc)^{2}}{2}]+[\frac{(ab)^{2}}{2}+\frac{(ca)^{2}}{2}]$$+[\frac{(bc)^{2}}{2}+\frac{(ca)^{2}}{2}]$+2[(ab)(bc)+(ab)(ca)+(bc)(ca)];
≥3[(ab)(bc)+(ab)(ca)+(bc)(ca)],当且仅当a=b=c时取“=”;
∴$(ab)(bc)+(ab)(ca)+(bc)(ca)≤\frac{1}{3}$,∴该选项错误.
故选:B.
点评 考查不等式a2+b2≥2ab的运用,注意判读等号能否取到,以及三个正数的算术-几何平均不等式的运用,并判断等号能否取到,不等式的性质,完全平方式的运用.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
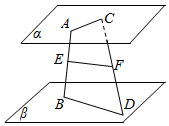 已知:如图,平面α、β满足α∥β,A、C∈α,B、D∈β,E∈AB,F∈CD,AC与BD异面,且$\frac{AE}{EB}=\frac{CF}{FD}$.求证:EF∥β
已知:如图,平面α、β满足α∥β,A、C∈α,B、D∈β,E∈AB,F∈CD,AC与BD异面,且$\frac{AE}{EB}=\frac{CF}{FD}$.求证:EF∥β查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com