
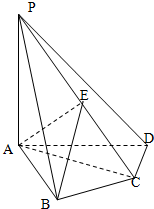
 在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.分析 (1)推导出PA⊥CD,从而CD⊥面PAC,由此能证明CD⊥AE.
(2)推导出PC⊥AE,CD⊥AE,由此能证明AE⊥面PDC.
(3)由题可知PA,AB,AD两两垂直,建立空间直角坐标系,利用向量法能求出二面角B-PC-D的余弦值.
解答 证明:(1)∵在四棱锥P-ABCD中,PA⊥底面ABCD,∴PA⊥CD.
又∵AC⊥CD,∴CD⊥面PAC,
∵AE?面PAC,∴CD⊥AE.…(4分)
(2)∵AB=BC,∠ABC=60°,∴△ABC是等边三角形,∴PA=AC,
又E是PC的中点,∴PC⊥AE,
又由(1)可知CD⊥AE,
∵CD∩PC=C,∴AE⊥面PDC.…(8分)
解:(3)由题可知 PA,AB,AD两两垂直,如图建立空间直角坐标系,
设AB=2,则$B(2,0,0),C(1,\sqrt{3},0),P(0,0,2)$,$D(0,\frac{4}{{\sqrt{3}}},0)$.
设面PBC的一个法向量为$\overrightarrow m=(x,y,z)$,
∵$\overrightarrow{PB}=(2,0,-2)$,$\overrightarrow{BC}=(-1,\sqrt{3,}0)$,
∴$\left\{{\begin{array}{l}{\overrightarrow{PB}•\overrightarrow m=0}\\{\overrightarrow{BC}•\overrightarrow m=0}\end{array}}\right.$,即$\left\{{\begin{array}{l}{2x-2z=0}\\{-x+\sqrt{3}y=0}\end{array}}\right.$,
取$y=\sqrt{3}$,则x=z=3,即$\overrightarrow m=(3,\sqrt{3},3)$,
设面PDC的一个法向量为$\overrightarrow n=(x,y,z)$,
∵$\overrightarrow{PC}=(1,\sqrt{3},-2)$,$\overrightarrow{PD}=(0,\frac{4}{{\sqrt{3}}},-2)$,
∴$\left\{{\begin{array}{l}{\overrightarrow{PC}•\overrightarrow n=0}\\{\overrightarrow{PD}•\overrightarrow n=0}\end{array}}\right.$,即$\left\{{\begin{array}{l}{x+\sqrt{3}y-2z=0}\\{\frac{4}{{\sqrt{3}}}y-2z=0}\end{array}}\right.$,
取$y=\sqrt{3}$则x=1,z=2,即$\overrightarrow n=(1,\sqrt{3},2)$,
$cos<\overrightarrow{m},\overrightarrow{n}>=\frac{{\overrightarrow{m}•\overrightarrow{n}}}{{|\overrightarrow{m}||\overrightarrow{n}|}}=\frac{3+3+6}{{\sqrt{21}\sqrt{8}}}=\frac{{\sqrt{42}}}{7}$,
由图可知二面角B-PC-D的余弦值为$-\frac{{\sqrt{42}}}{7}$.…(12分)
点评 本题考查异面直线垂直和线面垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | f(0)+f(2)<2f(1) | B. | f(0)+f(2)≤2f(1) | C. | f(0)+f(2)≥2f(1) | D. | f(0)+f(2)>2f(1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{π}{3},\frac{{\sqrt{3}}}{2}-\frac{π}{6})$ | B. | $(-\frac{π}{3},\frac{π}{6}-\frac{{\sqrt{3}}}{2})$ | C. | $x=\frac{π}{3}$ | D. | $x=-\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ②③ | C. | ①②③ | D. | ④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$-1或$\sqrt{3}$+1 | B. | $\sqrt{3}$-1 | C. | $\sqrt{3}$+1 | D. | 2-$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com