
分析 (Ⅰ)由二倍角公式和辅助角公式化简,由图象上两个相邻的最高点之间的距离为π,即可得到ω,由此得到单调增区间.
(Ⅱ)由f(θ)=$\frac{2}{3}$,得到$sin(2θ-\frac{π}{6})=\frac{1}{3}$.由此由二倍角公式得到结果.
解答 解:(Ⅰ)$f(x)=2\sqrt{3}sinωxcosωx-2{cos^2}ωx+1$
=$\sqrt{3}(2sinωxcosωx)-(2{cos^2}ωx-1)$=$\sqrt{3}sin2ωx-cos2ωx$=$2sin(2ωx-\frac{π}{6})$.
由题意知,函数f(x)的最小正周期为π,
则$\frac{2π}{2ω}=π$,故ω=1.
所以f(x)=$2sin(2x-\frac{π}{6})$,
由$2kπ-\frac{π}{2}≤2x-\frac{π}{6}≤2kπ+\frac{π}{2}(k∈Z)$,
得$kπ-\frac{π}{6}≤x≤kπ+\frac{π}{3}(k∈Z)$,
所以函数f(x)的单调递增区间为$[kπ-\frac{π}{6},kπ+\frac{π}{3}](k∈Z)$.
(Ⅱ)由f(x)=$2sin(2x-\frac{π}{6})$,
$f(θ)=\frac{2}{3}$,得$sin(2θ-\frac{π}{6})=\frac{1}{3}$.
$cos(\frac{π}{3}-4θ)=cos(4θ-\frac{π}{3})=cos2(2θ-\frac{π}{6})=1-2{sin^2}(2θ-\frac{π}{6})=1-2×\frac{1}{9}=\frac{7}{9}$.
点评 本题考查由二倍角公式和辅助角公式,以及数形结合,即可得到ω.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
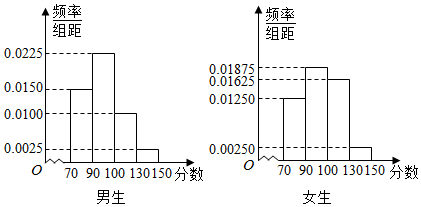
| 优秀生 | 非优秀生 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com