
【题目】已知函数![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)若函数![]() 在
在![]() 上是单调递增函数,求实数
上是单调递增函数,求实数![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,
时,![]() 无极值;当
无极值;当![]() 时,
时,![]() 有极小值为
有极小值为![]() ,无极大值
,无极大值
(2)![]()
【解析】
(1)根据解析式求得导函数![]() ,讨论
,讨论![]() 与
与![]() 两种情况下导函数的符号,即可由单调性判断函数的极值.
两种情况下导函数的符号,即可由单调性判断函数的极值.
(2)将![]() 的解析式代入可得
的解析式代入可得![]() ,并求得
,并求得![]() ,根据函数
,根据函数![]() 在
在![]() 上是单调递增函数可知
上是单调递增函数可知![]() ,分离参数并构造函数
,分离参数并构造函数![]() ,求得
,求得![]() ,即可判断
,即可判断![]() 在
在![]() 上的单调性,进而由恒成立问题解法求得
上的单调性,进而由恒成立问题解法求得![]() 的取值范围即可.
的取值范围即可.
(1)函数![]() .定义域为
.定义域为![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增,无极值.
上单调递增,无极值.
当![]() 时,令
时,令![]() ,解得
,解得![]() ,
,
若![]() ,解得
,解得![]() ;
;
若![]() ,解得
,解得![]() ,
,
所以![]() 在
在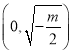 上单调递减,在
上单调递减,在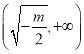 上单调递增,
上单调递增,
所以函数![]() 有极小值为
有极小值为 ,无极大值.
,无极大值.
综上,当![]() 时,
时,![]() 无极值;
无极值;
当![]() 时,
时,![]() 有极小值为
有极小值为![]() ,无极大值.
,无极大值.
(2)![]() ,
,![]()
因为函数![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,化简得
,化简得![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,
,![]() ,
,
即![]() 在
在![]() 上单调递减.
上单调递减.
又![]() ,所以
,所以![]() .
.
综上![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】一个几何体的三视图如图所示,正视图为等腰直角三角形,俯视图中虚线平分矩形的面积,则该几何体的体积为_____,其外接球的表面积为______.
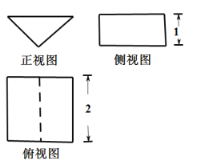
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的一个顶点为
的一个顶点为![]() ,离心率为
,离心率为![]() .
.
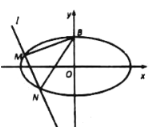
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭园C交于
与椭园C交于![]() ,
,![]() 两点,直线
两点,直线![]() 与线
与线![]() 的斜率之积为
的斜率之积为![]() ,证明:直线
,证明:直线![]() 过定点,并求
过定点,并求![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市环保部门为了让全市居民认识到冬天烧煤取暖对空气![]() 数值的影响,进而唤醒全市人民的环保节能意识。对该市取暖季烧煤天数
数值的影响,进而唤醒全市人民的环保节能意识。对该市取暖季烧煤天数![]() 与空气
与空气![]() 数值不合格的天数
数值不合格的天数![]() 进行统计分析,得出下表数据:
进行统计分析,得出下表数据:
| 9 | 8 | 7 | 5 | 4 |
| 7 | 6 | 5 | 3 | 2 |
(1)以统计数据为依据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)求出的线性回归方程,预测该市烧煤取暖的天数为20时空气![]() 数值不合格的天数.
数值不合格的天数.
参考公式: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知短轴长为2的椭圆![]() ,直线
,直线![]() 的横、纵截距分别为
的横、纵截距分别为![]() ,且原点到直线
,且原点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 经过椭圆的右焦点
经过椭圆的右焦点![]() 且与椭圆
且与椭圆![]() 交于
交于![]() 两点,若椭圆
两点,若椭圆![]() 上存在一点
上存在一点![]() 满足
满足![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
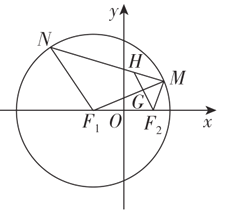
【题目】如图,已知点![]() ,点
,点![]() 均在圆
均在圆![]() 上,且
上,且![]() ,过点
,过点![]() 作
作![]() 的平行线分别交
的平行线分别交![]() ,
,![]() 于
于![]() 两点.
两点.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 的动直线
的动直线![]() 与点
与点![]() 的轨迹交于
的轨迹交于![]() 两点.问是否存在常数
两点.问是否存在常数![]() ,使得
,使得![]() 点为定值?若存在,求出
点为定值?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学先修课程,是在高中开设的具有大学水平的课程,旨在让学有余力的高中生早接受大学思维方式、学习方法的训练,为大学学习乃至未来的职业生涯做好准备.某高中成功开设大学先修课程已有两年,共有250人参与学习先修课程.
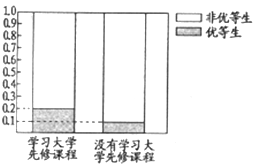
(Ⅰ)这两年学校共培养出优等生150人,根据下图等高条形图,填写相应列联表,并根据列联表检验能否在犯错的概率不超过0.01的前提下认为学习先修课程与优等生有关系?
优等生 | 非优等生 | 总计 | |
学习大学先修课程 | 250 | ||
没有学习大学先修课程 | |||
总计 | 150 |
(Ⅱ)某班有5名优等生,其中有2名参加了大学生先修课程的学习,在这5名优等生中任选3人进行测试,求这3人中至少有1名参加了大学先修课程学习的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式:![]() ,其中
,其中![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com