
分析 取AC的中点O,连结OB,OD,则∠BOD为所求二面角的平面角,求出OB,OD,在△OBD中使用余弦定理求出cos∠BOD.
解答 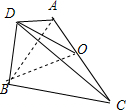 解:设菱形中心为O,连接OB,OD,
解:设菱形中心为O,连接OB,OD,
∵AB=BC=CD=AD=1,∠ABC=60°,
∴△ABC,△ACD是正三角形,
∵O是AC的中点,∴OB=OD=$\frac{\sqrt{3}}{2}$,
OB⊥AC,OD⊥AC,
∴∠BOD为二面角B-AC-D的平面角.
在△OBD中,由余弦定理得cos∠BOD=$\frac{O{B}^{2}+O{D}^{2}-B{D}^{2}}{2OB•OD}$=$\frac{1}{3}$.
故答案为$\frac{1}{3}$.
点评 本题考查了二面角的定义与计算,作出二面角的平面角是关键,属于中档题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知三次函数f(x)=ax3+bx2+cx+d的图象如图所示,则$\frac{f′(-2)}{f′(1)}$=( )
已知三次函数f(x)=ax3+bx2+cx+d的图象如图所示,则$\frac{f′(-2)}{f′(1)}$=( )| A. | 5 | B. | -5 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大于10.828 | B. | 小于7.829 | C. | 小于6.635 | D. | 大于2.706 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
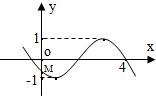 已知函数f(x)=Asin(ωx+φ)(x∈R),且A>0,ω>0,-π≤φ≤0.若f(x)的部分图象如图,且与y轴交点M(0,-$\frac{{\sqrt{2}}}{2}$),则ω+φ=-$\frac{5π}{16}$.
已知函数f(x)=Asin(ωx+φ)(x∈R),且A>0,ω>0,-π≤φ≤0.若f(x)的部分图象如图,且与y轴交点M(0,-$\frac{{\sqrt{2}}}{2}$),则ω+φ=-$\frac{5π}{16}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com