
分析 由A(0,t),B(0,t+6)(-5≤t≤-2),设AC斜率为k1,BC斜率为k2,推出直线AC、直线BC的方程,求出△ABC的面积S的表达式,求出面积的最大值和最小值.
解答 解:设AC斜率为k1,BC斜率为k2,则直线AC的方程为y=k1x+t,直线BC的方程为y=k2x+t+6.
由方程组$\left\{\begin{array}{l}{y={k}_{1}x+t}\\{y={k}_{2}x+t+6}\end{array}\right.$,得C点的横坐标为${x}_{c}=\frac{6}{{k}_{1}-{k}_{2}}$,
∵|AB|=t+6-t=6,∴S=$\frac{1}{2}$|$\frac{6}{{k}_{1}-{k}_{2}}$|•6=$\frac{18}{{k}_{1}-{k}_{2}}$,
由于圆M与AC相切,∴$\frac{|{k}_{1}+t|}{\sqrt{1+{{k}_{1}}^{2}}}=1$,∴${k}_{1}=\frac{1-{t}^{2}}{2t}$;
同理,${k}_{2}=\frac{1-(t+6)^{2}}{2(t+6)}$,∴${k}_{1}-{k}_{2}=\frac{3({t}^{2}+6t+1)}{{t}^{2}+6t}$,
∴S=$\frac{6({t}^{2}+6t)}{{t}^{2}+6t+1}=6(1-\frac{1}{{t}^{2}+6t+1})$,
∵-5≤t≤-2,∴-2≤t+3≤1,∴-8≤t2+6t+1≤-4,
∴${S}_{max}=6(1+\frac{1}{4})=\frac{15}{2}$,${S}_{min}=6(1+\frac{1}{8})=\frac{27}{4}$.
点评 本题考查直线与圆的位置关系,三角形面积的最值的求法,考查计算能力,是中档题.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:填空题
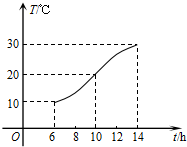 某地一天中6时至14时的温度变化曲线近似满足函数T=Asin(ωt+φ)+b(其中$\frac{π}{2}$<φ<π),6时至14时期间的温度变化曲线如图所示,它是上述函数的半个周期的图象,那么这一天6时至14时温差的最大值是20°C;图中曲线对应的函数解析式是y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].
某地一天中6时至14时的温度变化曲线近似满足函数T=Asin(ωt+φ)+b(其中$\frac{π}{2}$<φ<π),6时至14时期间的温度变化曲线如图所示,它是上述函数的半个周期的图象,那么这一天6时至14时温差的最大值是20°C;图中曲线对应的函数解析式是y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com