Question

19．在四棱锥P-ABCD中，AD⊥平面PDC，PD⊥DC，底面ABCD是梯形，AB∥DC，AB=AD=PD=1，CD=2
（1）求证：平面PBC⊥平面PBD；
（2）设Q为棱PC上一点，$\overrightarrow{PQ}$=λ$\overrightarrow{PC}$，试确定 λ的值使得二面角Q-BD-P为60°．

Answer 1

分析 （1）在梯形ABCD中，过点作B作BH⊥CD于H，通过面面垂直的判定定理即得结论；
（2）过点Q作QM∥BC交PB于点M，过点M作MN⊥BD于点N，连QN．则∠QNM是二面角Q-BD-P的平面角，在Rt三角形MNQ中利用tan∠MNQ=$\frac{QM}{MN}$计算即可．

解答 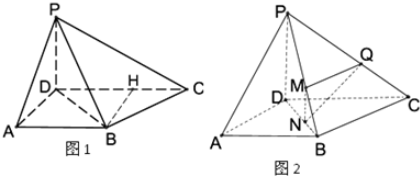（1）证明：∵AD⊥平面PDC，PD?平面PCD，DC?平面PDC，图1所示．
∴AD⊥PD，AD⊥DC，
在梯形ABCD中，过点作B作BH⊥CD于H，
在△BCH中，BH=CH=1，∴∠BCH=45°，
又在△DAB中，AD=AB=1，∴∠ADB=45°，
∴∠BDC=45°，∴∠DBC=90°，∴BC⊥BD．
∵PD⊥AD，PD⊥DC，AD∩DC=D．
AD?平面ABCD，DC?平面ABCD，
∴PD⊥平面ABCD，
∵BC?平面ABCD，∴PD⊥BC，
∵BD∩PD=D，BD?平面PBD，PD?平面PBD．
∴BC⊥平面PBD，
∵BC?平面PBC，∴平面PBC⊥平面PBD；
（2）解：过点Q作QM∥BC交PB于点M，过点M作MN⊥BD于点N，连QN．
由（1）可知BC⊥平面PDB，∴QM⊥平面PDB，∴QM⊥BD，
∵QM∩MN=M，∴BD⊥平面MNQ，∴BD⊥QN，图2所示．
∴∠QNM是二面角Q-BD-P的平面角，∴∠QNM=60°，
∵$\overrightarrow{PQ}=λ\overrightarrow{PC}$，∴$\frac{PQ}{PC}=λ$，
∵QM∥BC，∴$\frac{PQ}{PC}=\frac{QM}{BC}=\frac{PM}{PB}=λ$，∴QM=λBC，
由（1）知$BC=\sqrt{2}$，∴$QM=\sqrt{2}λ$，
又∵PD=1，MN∥PD，∴$\frac{MN}{PD}=\frac{BM}{PB}$，
∴MN=$\frac{BM}{PB}=\frac{PB-PM}{PB}$=$1-\frac{PM}{PB}$=1-λ，
∵tan∠MNQ=$\frac{QM}{MN}$，∴$\frac{\sqrt{2}λ}{1-λ}=\sqrt{3}$，
∴$λ=3-\sqrt{6}$．

点评 本题考查二面角，空间中面与面的位置关系，注意解题方法的积累，属于中档题．