练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．直线y=a与y=tanx的图象的相邻两个交点的距离是（　　）
    A．$\frac{π}{2}$B．π
    C．2πD．与a的值的大小有关

    分析 根据正切函数的周期性进行求解．

    解答 解：直线y=a与y=tanx的图象的相邻两个交点的距离是一个周期，
    ∴y=tanx的最小正周期T=π，
    ∴直线y=a与y=tanx的图象的相邻两个交点的距离是π，
    故选：B．

    点评 本题主要考查正切函数的周期性，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

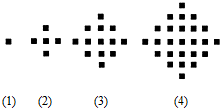    11．某少数民族的刺绣有着悠久的历史，如图（1）、（2）、（3）、（4）为她们刺绣最简单的四个图案，这些图案都由小正方形构成，小正方形数越多刺绣越漂亮，现按同样的规律刺绣（小正方形的摆放规律相同），设第n个图形包含f（n）个小正方形．
    （1）求出f（2），f（3）f（4）f（5）并猜测f（n）的表达式；
    （2）求证：$\frac{1}{f（1）}$+$\frac{1}{f（2）-1}$+$\frac{1}{f（3）-1}$+…+$\frac{1}{f（n）-1}$$＜\frac{3}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知MOD函数是一个求余函数，其格式为MOD（n，m），其结果为n除以m的余数，例如MOD（8，3）=2．如图是一个算法的程序框图，当输入的值为36时，则输出的结果为（　　）
    A．6B．7C．8D．9

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知函数g（x）=x-$\sqrt{3x+1}，h（x）=\frac{1}{2x}+\sqrt{3x+1}$，那么函数f（x）=g（x）+h（x）的解析式是f（x）=x+$\frac{1}{2x}$，（x≥-$\frac{1}{3}$，且x≠0）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知函数f（x）=1-$\sqrt{1-x}$
    （1）证明：函数f（x）在定义域上是增函数．
    （2）求函数f（x）在[-3，0]上的最大值与最小值．
    （3）求函数的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．如图，若f（x）=log3x，g（x）=log2x，输入x=0.25，则输出h（x）=（　　）
    A．0.25B．$\frac{1}{2}$log322C．-21log32D．-2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知a＜0，解关于x的不等式ax2-（a-2）x-2＜0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．一次选拔运动员，测得7名选手的身高（单位：cm）分布茎叶图如图所示，已知记录的平均身高为177cm，有1名选手的身高记录不清楚，其末位数记为x，那么x的值为（　　）
    A．7B．6C．5D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知A，B是抛物线y2=4x上异于顶点O的两个点，直线OA与直线OB的斜率之积为定值-4，F为抛物线的焦点，△AOF，△BOF的面积分别为S1，S2，则S12+S22的最小值为（　　）
    A．8B．6C．4D．2

    查看答案和解析>>

    同步练习册答案