
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点为圆
,右焦点为圆![]() 的圆心,且圆
的圆心,且圆![]() 截
截![]() 轴所得弦长为4.
轴所得弦长为4.
(1)求椭圆![]() 与圆
与圆![]() 的方程;
的方程;
(2)若直线![]() 与曲线
与曲线![]() ,
,![]() 都只有一个公共点,记直线
都只有一个公共点,记直线![]() 与圆
与圆![]() 的公共点为
的公共点为![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1) 椭圆![]() 的方程为
的方程为![]() ;圆
;圆![]() 的方程为
的方程为![]() . (2)
. (2) ![]() 或
或![]() .
.
【解析】
(1)由椭圆的离心率为![]() ,右焦点为圆C2:(x﹣1)2+y2=r2的圆心,列出方程组,求出a,b,c,由此能求出椭圆
,右焦点为圆C2:(x﹣1)2+y2=r2的圆心,列出方程组,求出a,b,c,由此能求出椭圆![]() 的方程;由圆
的方程;由圆![]() 截y轴所得弦长为4,得
截y轴所得弦长为4,得![]() =22+12=5,由此能求出圆
=22+12=5,由此能求出圆![]() 的方程.(2)设直线l的方程为y=kx+m,推导出4k2﹣m2=2km﹣5,由
的方程.(2)设直线l的方程为y=kx+m,推导出4k2﹣m2=2km﹣5,由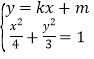 ,得(3+4k2)x2+8kmx+4m2﹣12=0,由此利用根的判别式、直线方程、圆、椭圆性质,结合已知条件能求出直线l与圆
,得(3+4k2)x2+8kmx+4m2﹣12=0,由此利用根的判别式、直线方程、圆、椭圆性质,结合已知条件能求出直线l与圆![]() 的公共点A的坐标.
的公共点A的坐标.
(1)由题意知:![]() 解得
解得![]()
又![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
因为圆![]() 截
截![]() 轴所得弦长为4,所以
轴所得弦长为4,所以![]() ,
,
所以圆![]() 的方程为
的方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,则
,则
![]() ,
,
即![]() ①
①
由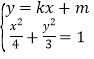 得
得![]() ,
,
因为直线![]() 与曲线
与曲线![]() 只有一个公共点,所以
只有一个公共点,所以
![]() ,
,
化简,得 ![]() ②
②
①②联立,解得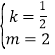 或
或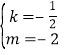
由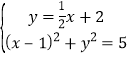 解得
解得![]() ,
,
由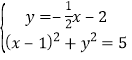 解得
解得![]() ,
,
故直线![]() 与圆
与圆![]() 的公共点
的公共点![]() 的坐标为
的坐标为![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】党的十八大以来,我国精准扶贫已经实施了六年,我国贫困人口从2012年的9899万人,减少到2018年的1660万人,2019年将努力实现减少贫困人口1000万人以上的目标,力争2020年在现行标准下,农村贫困人口全部脱贫,贫困县全部脱贫摘帽.某市为深入分析该市当前扶贫领域存在的突出问题,市扶贫办近三年来,每半年对贫困户(用![]() 表示,单位:万户)进行取样,统计结果如图所示,从2016年6月底到2019年6月底的共进行了七次统计,统计时间用序号
表示,单位:万户)进行取样,统计结果如图所示,从2016年6月底到2019年6月底的共进行了七次统计,统计时间用序号![]() 表示,例如:2016年12月底(时间序号为2)贫困户为5.2万户.
表示,例如:2016年12月底(时间序号为2)贫困户为5.2万户.

(1)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测到2020年12月底,该市能否实现贫困户全部脱贫;
,并预测到2020年12月底,该市能否实现贫困户全部脱贫;
(2)为尽快打赢脱贫攻坚战,该市扶贫办在2019年6月底时,对全市贫困户随机抽取了100户贫困户,对每个家庭最主要经济收入来源进行抽样调查,统计结果如图.并决定据此选派一批农业技术人员对全市所有贫困户中,家庭最主要经济收入来源为养殖收入和种植收入的贫困户进行对口帮扶,每一名农业技术人员对口帮扶贫困户90户,则该市应分别安排多少农业技术人员对家庭最主要经济收入来源为养殖收入和种植收入的贫困户进行对口帮扶?
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程为ρ2=![]() .
.
(1)若以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,求曲线C的直角坐标方程;
(2)若P(x,y)是曲线C上的一个动点,求3x+4y的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]()
![]() ,过直线
,过直线![]() :
:![]() 上任一点
上任一点![]() 向抛物线
向抛物线![]() 引两条切线
引两条切线![]() (切点为
(切点为![]() ,且点
,且点![]() 在
在![]() 轴上方).
轴上方).
(1)求证:直线![]() 过定点,并求出该定点;
过定点,并求出该定点;
(2)抛物线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有下述四个结论:①若
有下述四个结论:①若![]() ,则
,则![]() ;②
;②![]() 的图象关于点
的图象关于点![]() 对称;③函数
对称;③函数![]() 在
在![]() 上单调递增;④
上单调递增;④![]() 的图象向右平移
的图象向右平移![]() 个单位长度后所得图象关于
个单位长度后所得图象关于![]() 轴对称.其中所有正确结论的编号是( )
轴对称.其中所有正确结论的编号是( )
A.①②④B.①②C.③④D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】庙会是我国古老的传统民俗文化活动,又称“庙市”或 “节场”.庙会大多在春节、元宵节等节日举行.庙会上有丰富多彩的文化娱乐活动,如“砸金蛋”(游玩者每次砸碎一颗金蛋,如果有奖品,则“中奖”).今年春节期间,某校甲、乙、丙、丁四位同学相约来到某庙会,每人均获得砸一颗金蛋的机会.游戏开始前,甲、乙、丙、丁四位同学对游戏中奖结果进行了预测,预测结果如下:
甲说:“我或乙能中奖”; 乙说:“丁能中奖”;
丙说:“我或乙能中奖”; 丁说:“甲不能中奖”.
游戏结束后,这四位同学中只有一位同学中奖,且只有一位同学的预测结果是正确的,则中奖的同学是( )

A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com