
| A. | a<-1或a>3 | B. | -1<a<3 | C. | -1≤a≤3 | D. | a≤-1或a≥3 |
分析 不存在实数x使不等式|x-1|+|x-3|≤a2-2a-1成立??x∈R,使不等式|x-1|+|x-3|>a2-2a-1恒成立,再构造函数f(x)=|x-1|+|x-3|,求得f(x)min,依题意得:a2-2a-1<f(x)min,解之即可得到答案.
解答 解:不存在实数x使不等式|x-1|+|x-3|≤a2-2a-1成立??x∈R,使不等式|x-1|+|x-3|>a2-2a-1恒成立,
构造函数f(x)=|x-1|+|x-3|,则a2-2a-1<f(x)min.
因为:|x-1|+|x-3|≥|(x-1)-(x-3)|=2,
所以,f(x)min=2,
所以,a2-2a-1<2,
解得:-1<a<3.
故选:B.
点评 本题考查函数恒成立问题,深刻理解题意,将“不存在实数x使不等式|x-1|+|x-3|≤a2-2a-1成立”等价转化为“?x∈R,使不等式|x-1|+|x-3|>a2-2a-1恒成立”是关键,考查构造法与绝对值不等式的应用,属于中档题,易错题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{9}$ | B. | -9 | C. | $\frac{1}{9}$ | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
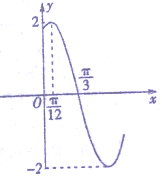 f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,把f(x)的图象向右平移$\frac{π}{3}$个单位长度得到g(x)的图象,则g(x)的单调递增区间为( )
f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,把f(x)的图象向右平移$\frac{π}{3}$个单位长度得到g(x)的图象,则g(x)的单调递增区间为( )| A. | [-$\frac{5π}{12}$+kπ,$\frac{π}{12}$+kπ](k∈Z) | B. | [-$\frac{π}{6}$+kπ,$\frac{π}{3}$+kπ](k∈Z) | ||
| C. | [-$\frac{π}{12}$+kπ,$\frac{5π}{12}$+kπ](k∈Z) | D. | [-$\frac{π}{6}$+kπ,$\frac{5π}{6}$+kπ](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{9},\frac{1}{3})$ | B. | $(-1,-\frac{1}{3})$ | C. | $(-1,-\frac{1}{3})∪(\frac{1}{9},\frac{1}{3})$ | D. | $[{-1,-\frac{1}{3}}]∪[{\frac{1}{9},\frac{1}{3}}]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com