
分析 (I)设AB方程为y=kx+a,与圆的方程联立得(1+k2)x2+(2ak-4)x+a2+3=0,由此利用韦达定理,结合已知条件能求出点P轨迹方程.
(II)求出圆心E到直线MN的距离,得$|{MN}|=2\sqrt{1-{h^2}}$,由此能求出S△EMN的最大值.
解答 解:(I)设AB方程为y=kx+a,与圆的方程联立得(1+k2)x2+(2ak-4)x+a2+3=0
设B,C两点坐标分别为(x1,y1),(x2,y2),
则${x_1}+{x_2}=-\frac{2ak-4}{{1+{k^2}}}$,${x_1}{x_2}=\frac{{{a^2}+3}}{{1+{k^2}}}$…(2分)
设P点坐标为(x,y),∵$\frac{BP}{PC}=\frac{AB}{AC}$,∴$\frac{{x-{x_1}}}{{{x_2}-x}}=\frac{x_1}{x_2}$…(3分)
∴$x=\frac{{2{x_1}{x_2}}}{{{x_1}+{x_2}}}=\frac{{{a^2}+3}}{2-ak}$,∴$y=kx+a=\frac{2a+3k}{2-ak}$…(4分)
消去k,得2x-ay-3=0,
∴点P轨迹方程是2x-ay-3=0(在圆内部分).…(6分)
(II)圆心E到直线MN的距离为$h=\frac{1}{{\sqrt{{a^2}+4}}}$…(7分)
∴$|{MN}|=2\sqrt{1-{h^2}}$…(8分)
∴${S_{△EMN}}=\frac{1}{2}•2\sqrt{1-{h^2}}•h=\sqrt{{h^2}(1-{h^2})}=\sqrt{-{h^4}+{h^2}}=\sqrt{-{{({h^2}-\frac{1}{2})}^2}+\frac{1}{4}}$….(10分)
∵$h∈(0,\frac{1}{2}]$∴当$h=\frac{1}{2}$时,S△EMN取得最大,最大值为$\frac{{\sqrt{3}}}{4}$.…(12分)
点评 本题考查点的轨迹方程的求法,考查三角形面积的最大值的求法,是中档题,解题时要认真审题,注意韦达定理、弦长公式的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
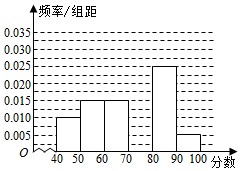 某校从参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如图所示的部分频率分布直方图.在统计方法中,同一组数据常用该组区间的中点值作为代表,观察图形的信息,据此估计本次考试的平均分为71.
某校从参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如图所示的部分频率分布直方图.在统计方法中,同一组数据常用该组区间的中点值作为代表,观察图形的信息,据此估计本次考试的平均分为71.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com