
分析 ①当k=3时,可化l的方程为x+y-6=0,由点到直线的距离公式和三角函数的最值可得;
②分别化为普通方程x2+y2=2,x+y-k=0,由直线l与圆C相交可得圆心O到直线l的距离d<$\sqrt{2}$,解关于k的不等式可得.
解答 解:①当k=3时,l:ρcos(θ-$\frac{π}{4}$)=3$\sqrt{2}$,
可得l:ρcosθcos$\frac{π}{4}$+ρsinθsin$\frac{π}{4}$=3$\sqrt{2}$,
整理得l:x+y-6=0,
则d=$\frac{|\sqrt{2}cosθ+\sqrt{2}sinθ-6|}{\sqrt{2}}$=$\frac{|2sin(θ+\frac{π}{4})-6|}{\sqrt{2}}$
∴当sin(θ+$\frac{π}{4}$)=-1时,dmax=$\frac{8}{\sqrt{2}}$=4$\sqrt{2}$;
②消去cosθ可将圆C的参数方程化为普通方程x2+y2=2,
直线l的极坐标方程化为普通方程x+y-k=0,
∵直线l与圆C相交,∴圆心O到直线l的距离d<$\sqrt{2}$,
即$\frac{|-k|}{\sqrt{2}}$<$\sqrt{2}$,解得-2<k<2.
点评 本题考查参数方程和极坐标方程,涉及点到直线的距离公式以及直线和圆的位置关系,属中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 25+15$\sqrt{3}$ | B. | 20+3$\sqrt{15}$ | C. | 15+3$\sqrt{3}$ | D. | 22+3$\sqrt{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 轿车A | 轿车B | 轿车C | |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
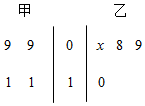 从甲、乙两个班级分别抽取4名同学的年龄制作出如右图所示的茎叶图,乙班的记录中有一个数据模糊,无法确认,在图中以X表示,已知这8个同学的平均年龄是9.5岁.
从甲、乙两个班级分别抽取4名同学的年龄制作出如右图所示的茎叶图,乙班的记录中有一个数据模糊,无法确认,在图中以X表示,已知这8个同学的平均年龄是9.5岁.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | 4 | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com