
| A�� | 7 | B�� | 4 | C�� | 3 | D�� | 2 |
���� ���ġ�3������x��ֵ���õ�����Ϊ��26������y��ֵ����æ�=3�������Ӧ��ϵΪ��y=x3-1�����˹�������ԭ�������ģ�
��� �⣺�������֪���ġ�3������x=3���õ�����Ϊ��26������y=26����æ�=3�������Ӧ��ϵΪ��y=x3-1��
���ܷ��ӵ�����Ϊ��7������y=7����ԭ����������x=2��
��ѡ��D��
���� ���⿼����ָ����������ʽ����ϸ�������⣬�ǽ����Ŀ�Ĺؼ����ǻ����⣮


 ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д�
ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��������ABCD-A1B1C1D1���ⳤΪ1��PΪBC���е㣬QΪ�߶�CC1�ϵĶ��㣬���� A��P��Q��ƽ��ظ����������õĽ����ΪS��������������ȷ���ǣ�������
��ͼ��������ABCD-A1B1C1D1���ⳤΪ1��PΪBC���е㣬QΪ�߶�CC1�ϵĶ��㣬���� A��P��Q��ƽ��ظ����������õĽ����ΪS��������������ȷ���ǣ�������| A�� | �٢� | B�� | �٢ڢ� | C�� | �ڢۢ� | D�� | �٢ڢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
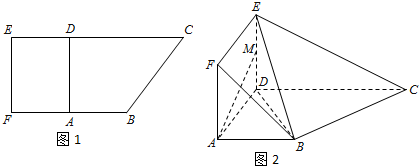
 ��ͼ����֪����P-ABCD�У�����ABCD��ƽ���ı��Σ�BC��ƽ��PAB��PA��AB��MΪPB���е㣬PA=AD=2��AB=1��
��ͼ����֪����P-ABCD�У�����ABCD��ƽ���ı��Σ�BC��ƽ��PAB��PA��AB��MΪPB���е㣬PA=AD=2��AB=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪�ڳ�����ABCD-A1B1C1D1�У�AD=A1A=$\frac{1}{2}$AB=2����E����AB��һ�㣬��$\frac{AE}{EB}$=�ˣ�
��ͼ����֪�ڳ�����ABCD-A1B1C1D1�У�AD=A1A=$\frac{1}{2}$AB=2����E����AB��һ�㣬��$\frac{AE}{EB}$=�ˣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com