练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设P是抛物线y＝x2上的点，若P点到直线2x－y－4＝0的距离最小，则P点的坐标为________．


    　(1,1)

    [解析]　解法1：设P点坐标为(x0，x)，由点到直线的距离公式得d＝＝|x－2x0＋4|

    ＝|(x0－1)2＋3|≥.

    由上式可知当x0＝1时，dmin＝.

    ∴点P的坐标为(1,1)．

    解法2：如图，平移2x－y－4＝0这条直线至过点P与抛物线相切，则P点到直线的距离最短．

    设P(x0，y0)，∵y′＝2x.

    ∴过P点的切线斜率k＝y′|x＝x0＝2x0＝2.

    ∴x0＝1，y0＝x＝1，故P点坐标为(1,1)．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知集合A＝{(x，y)|x，y为实数，且x2＋y2＝1}，B＝{(x，y)|x，y为实数，且x＋y＝1}，则A∩B的元素个数为(　　)

    A．4                                                             B．3

    C．2                                                             D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    (2013·琼海一模)如图，在正方体ABCD－A1B1C1D1中，E，F，G，H，M分别是棱AD，DD1，D1A1，A1B，AB的中点，点N在正方形EFGH的四边及其内部运动，则当N只需满足条件________时，就有MN⊥A1C1；当N只需满足条件________时，就有MN∥平面B1D1C.

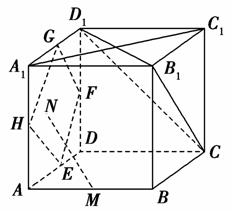
    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知点A(2,0)，抛物线C：x2＝4y的焦点为F，射线FA与抛物线C相交于点M，与其准线相交于点N，则|FM|：|MN|＝(　　)

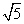    A．2:                                                      B．1:2

    C．1: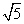                                                      D．1:3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设抛物线y2＝8x的焦点为F，准线为l，P为抛物线上一点，PA⊥l，A为垂足．如果直线AF的斜率为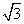－，那么|PF|＝(　　)

    A．4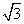                                                       B．8

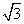    C．8                                                       D．16

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    为了了解参加一次知识竞赛的3204名学生的成绩，决定采用系统抽样的方法抽取一个容量为80的样本，那么总体中应随机剔除的个体数目是(　　)

    A．2　　　　                                                 B．3　　　　

    C．4　　　　                                                 D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用系统抽样法要从160名学生中抽取容量为20的样本，将160名学生随机地从1～160编号，按编号顺序平均分成20组(1～8号，9～16号，…，153～160号)，若第16组抽出的号码为126，则第1组中用抽签方法确定的号码是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某班的全体学生参加英语测试，成绩的频率分布直方图如图，数据的分组依次为：[20,40)，[40,60)，[60,80)，[80,100]．若低于60分的人数是15，则该班的学生人数是(　　)

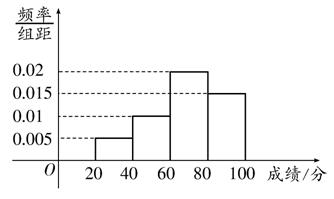
    A．45                                                           B．50 

    C．55                                                            D．60

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某中学研究性学习小组，为了考查高中学生的作文水平与爱看课外书的关系，在本校高三年级随机调查了50名学生．调查结果表明：在爱看课外书的25人中有18人作文水平好，另7人作文水平一般；在不爱看课外书的25人中有6人作文水平好，另19人作文水平一般．

    (1)试根据以上数据完成以下2×2列联表，并运用独立性检验思想，指出有多大把握认为中学生的作文水平与爱看课外书有关系？

    高中学生的作文水平与爱看课外书的2×2列联表

     

    爱看课外书

    不爱看课外书

    总计

    作文水平好

    作文水平一般

    总计

    (2)将其中某5名爱看课外书且作文水平好的学生分别编号为1、2、3、4、5，某5名爱看课外书且作文水平一般的学生也分别编号为1、2、3、4、5，从这两组学生中各任选1人进行学习交流，求被选取的两名学生的编号之和为3的倍数或4的倍数的概率．

    附表：

    P(K2≥k)或P(χ2≥k)

    0.50

    0.40

    0.25

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    k

    0.455

    0.708

    1.323

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    K2(或χ2)＝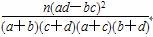

    查看答案和解析>>

    同步练习册答案