考点:命题的真假判断与应用
专题:等差数列与等比数列,简易逻辑
分析:写出等差数列的前n项和后变形得到
=a1+(n-1),由此得到命题①正确;由题意求出等差数列的公差小于0说明S
1、S
2、…、S
n这n个数中必有一个最小值得到②错;举特例说明③错;由数列递推式可得{a
n}是等比数列;举特殊数列说明⑤错.
解答:
解:对于①,由等差数列前n项和公式
Sn=na1+d,
知
=a1+(n-1),即数列
{}为等差数列,则已知三点都在一次函数
y=a1+(x-1)得图象上,故①对;
对于②,由a
3+a
7=-6得2a
1+8d=-6,又a
1=-11<0,
∴d=2>0,故S
1、S
2、…、S
n这n个数中必有一个最小值,故②错;
对于③,
Sm=a1+a2+…+am=a1(),
S2m-Sm=am+1+am+2+…+a2m=qm(a1+a2+…+am)=a1(),
S3m-S2m=a2m+1+a2m+2+…+a3m=q2m(a1+a2+…+am)=a1(),
当a
1+a
2+…+a
m≠0时是等比数列,当a
1+a
2+…+a
m=0时,命题不成立.故③错;
对于④由S
n+1=a
1+qS
n得S
n=a
1+qS
n-1,两式相减得a
n+1=qa
n,故④对;
对于⑤,若等比数列{a
n}的是常数数列,又a
1=1,则数列
{an2}是公比为1,首项为a
1=1的等比数列,则1-q
2=0,故⑤错.
故答案为:①④.
点评:本题考查了等差(比)数列的定义及前n项和公式的应用,考查了性质am=anqm-n(m,n∈N*)的应用,训练了等差数列前n项和公式的最值问题,是中档题.



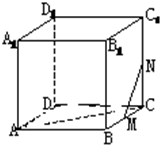 在正方体ABCD-A1B1C1D1中,求证:
在正方体ABCD-A1B1C1D1中,求证: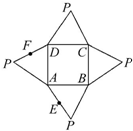 如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,在此几何体中,给出下面四个结论:
如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,在此几何体中,给出下面四个结论: