
分析 (1)令f(x)=t,根据f(x)的函数图象判断f(x)=t的解的个数,得出t=1为方程t2+at+b=0的解.
(2)当f(x)=t,t>0且t≠1时,关于x的方程f2(x)+af(x)+b=0有9个不同实数解,据此即可求得实数a的取值范围.
解答 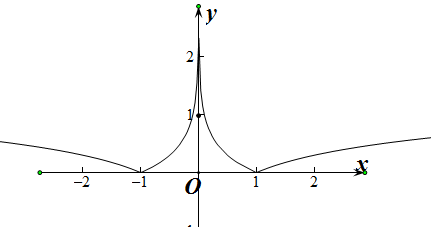 解:(1)做出f(x)的函数图象如图所示:
解:(1)做出f(x)的函数图象如图所示:
设f(x)=t,则当t=1时,f(x)=t有5个解,当t≠1时,f(x)=t有4个解.
∵关于x的方程f2(x)+af(x)+b=0有9个不同的实数解,
∴关于t的方程t2+at+b=0有两解,且t=1是其中一解,
∴1+a+b=0,即a+b=-1.
(2)当f(x)=t,t>0且t≠1时,关于x的方程f2(x)+af(x)+b=0有9个不同实数解,
∴t2+at-1-a=0,
∴a=-1-t,∵t>0且t≠1,
∴a∈(-∞,-2)∪(-2,-1)
点评 本题考查了方程的根与函数图象的关系,数形结合是数学解题中常用的思想方法,能够变抽象思维为形象思维,有助于把握数学问题的本质;另外,由于使用了数形结合的方法,很多问题便迎刃而解,且解法简捷.属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3} | B. | {-2,-1,0,1,2} | C. | {1,2} | D. | {-2,-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,一个空间几何体的正视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,那么这个几何体的体积为( )
如图所示,一个空间几何体的正视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,那么这个几何体的体积为( )| A. | 4π | B. | 2π | C. | $\frac{4π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,+∞) | B. | (-∞,0)∪(0,+∞) | C. | (-∞,0),(0,+∞) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com