Question

13．已知点C是线段AB上一点，$\overrightarrow{AC}$=2$\overrightarrow{CB}$，$\frac{\overrightarrow{MA}•\overrightarrow{MC}}{|\overrightarrow{MA}|}$=$\frac{\overrightarrow{MB}•\overrightarrow{MC}}{\overrightarrow{|MB|}}$，则$\frac{\overrightarrow{MA}•\overrightarrow{MB}}{|AB{|}^{2}}$的最大值为2．

Answer 1

分析 由已知可得$|\overrightarrow{MA}|=2|\overrightarrow{MB}|$，然后以AB所在直线为x轴，以C为坐标原点距离平面直角坐标系，设点A、B、M的坐标，利用数量积的坐标运算求得答案．

解答 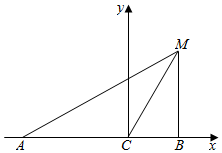解：由$\frac{\overrightarrow{MA}•\overrightarrow{MC}}{|\overrightarrow{MA}|}$=$\frac{\overrightarrow{MB}•\overrightarrow{MC}}{\overrightarrow{|MB|}}$，得$\frac{|\overrightarrow{MA}|•|\overrightarrow{MC}|cos∠AMC}{|\overrightarrow{MA}|}=\frac{|\overrightarrow{MB}|•|\overrightarrow{MC}|cos∠BMC}{|\overrightarrow{MB}|}$，
∴cos∠AMC=cos∠BMC，即∠AMC=∠BMC，
又$\overrightarrow{AC}$=2$\overrightarrow{CB}$，∴$|\overrightarrow{MA}|=2|\overrightarrow{MB}|$，
如图：设|AB|=3a，
以AB所在直线为x轴，以C为坐标原点距离平面直角坐标系，
则A（-a，0），B（a，0），
再设M（m，n），
由$|\overrightarrow{MA}|=2|\overrightarrow{MB}|$，得$\sqrt{（-2a-m）^{2}+{n}^{2}}=2\sqrt{（a-m）^{2}+{n}^{2}}$，
整理得：m²+n²=4ma ①，
又$\overrightarrow{MA}•\overrightarrow{MB}=（-2a-m，-n）•（a-m，-n）$=5ma-2a²，
∴$\frac{\overrightarrow{MA}•\overrightarrow{MB}}{|AB{|}^{2}}$=$\frac{5ma-2{a}^{2}}{9{a}^{2}}$=$\frac{5m}{9a}-\frac{2}{9}$，
又由①知：M的轨迹为（m-2a）²+n²=4a²，∴m≤4a，
∴$\frac{\overrightarrow{MA}•\overrightarrow{MB}}{|AB{|}^{2}}$$≤\frac{20a}{9a}-\frac{2}{9}=2$．
故答案为：2．

点评 本题考查平面向量的数量积运算，考查数学转化思想方法，考查推理论证能力和运算能力，难度较大．