
分析 (1)直接利用奇函数的定义列式求得a值;
(2)函数f(x)=a-$\frac{2}{{{2^x}+1}}$为(-∞,+∞)上的增函数.利用函数的单调性定义证明;
(3)把f(x)>1-x在[0,+∞)上恒成立,转化为a-$\frac{2}{{{2^x}+1}}$>1-x在[0,+∞)上恒成立,即a>$\frac{2}{{{2^x}+1}}$+1-x在[0,+∞)上恒成立,构造函数g(x)=$\frac{2}{{{2^x}+1}}$+1-x,利用导数求其最大值得a的范围.
解答 解:(1)∵函数f(x)=a-$\frac{2}{{{2^x}+1}}$为奇函数,
∴f(-x)+f(x)=$a-\frac{2}{{2}^{-x}+1}+a-\frac{2}{{2}^{x}+1}=2a-\frac{{2}^{x+1}}{{2}^{x}+1}-\frac{2}{{2}^{x}+1}$=$2a-\frac{2({2}^{x}+1)}{{2}^{x}+1}=2(a-1)=0$恒成立,得a=1;
(2)函数f(x)=a-$\frac{2}{{{2^x}+1}}$为(-∞,+∞)上的增函数.
证明:设x1,x2∈(-∞,+∞),且x1<x2,
则f(x1)-f(x2)=$a-\frac{2}{{2}^{{x}_{1}}+1}-a+\frac{2}{{2}^{{x}_{2}}+1}$=$\frac{2}{{2}^{{x}_{2}}+1}-\frac{2}{{2}^{{x}_{1}}+1}=\frac{2({2}^{{x}_{1}}-{2}^{{x}_{2}})}{({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}$,
∵x1<x2,∴${2}^{{x}_{1}}-{2}^{{x}_{2}}<0$,$({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)>0$,
则$\frac{2({2}^{{x}_{1}}-{2}^{{x}_{2}})}{({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}<0$,∴f(x1)<f(x2),即函数f(x)=a-$\frac{2}{{{2^x}+1}}$为(-∞,+∞)上的增函数;
(3)若f(x)>1-x在[0,+∞)上恒成立,则a-$\frac{2}{{{2^x}+1}}$>1-x在[0,+∞)上恒成立,
即a>$\frac{2}{{{2^x}+1}}$+1-x在[0,+∞)上恒成立,
令g(x)=$\frac{2}{{{2^x}+1}}$+1-x,则g′(x)=$\frac{-{2}^{x+1}ln2}{({2}^{x}+1)^{2}}-1$<0,
∴g(x)=$\frac{2}{{{2^x}+1}}$+1-x在[0,+∞)上为减函数,则f(x)max=g(0)=2.
∴a>2.
点评 本题考查函数奇偶性的性质,考查了恒成立问题的求解方法,训练了分离变量法,是中档题.


科目:高中数学 来源: 题型:解答题
学科 学生 | A | B | C | D | E |
| 数学成绩x | 88 | 76 | 73 | 66 | 63 |
| 物理成绩Y | 78 | 68 | 70 | 64 | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
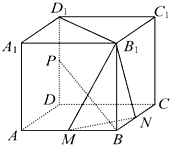 如图,正方体ABCD-A1B1C1D1中,P,M,N分别为棱DD1,AB,BC的中点.
如图,正方体ABCD-A1B1C1D1中,P,M,N分别为棱DD1,AB,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 公差为d的等差数列 | B. | 公差为cd的等差数列 | ||
| C. | 不是等差数列 | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
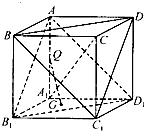 如图,ABCD-A1B1C1D1是棱长为a的正方体,有下列说法:
如图,ABCD-A1B1C1D1是棱长为a的正方体,有下列说法:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com