Question

15．已知定点D（1，0），M是圆C：（x+1）²+y²=16上任意一点，线段MD的中垂线与半径MC交于点P，设动点P的轨迹为曲线R．
（1）求曲线R的方程；
（2）若直线l与圆O：x²+y²=1相切，与曲线R相交于A，B两点，求△AOB面积的取值范围．

Answer 1

分析 （1）由题意求出圆C的圆心坐标、半径，画出图象连接PD，结合圆的定义和垂直平分线的性质列出方程，由椭圆的定义判断出曲线R的形状，由椭圆的标准方程求出轨迹方程；
（2）当直线l的斜率不为零时，设直线l的方程为x=my+n，由直线和圆相切的条件：d=r，由点到直线的距离公式列出方程，化简可得m、n的关系，联立直线方程和椭圆方程，运用韦达定理和弦长公式求出|AB|，由换元法和函数的性质求出△AOB的面积取值范围，当直线l的斜率为零，求出直线方程和|AB|，可得△AOB的面积，综合起来可得答案．

解答 解：（1）∵圆C方程为：（x+1）²+y²=16，∴点C（-1，0），半径R=4，
∵线段MD的中垂线与线段CM相交于点P，连结PD，
∴|PM|=|PD|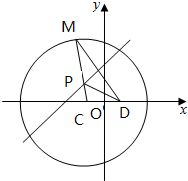，则|CP|+|PD|=|CP|+|PM|=4＞|CD|，
∴P的轨迹R是以C，D为焦点，长轴长为4的椭圆，
则a=2，c=1，即b=$\sqrt{{a}^{2}-{c}^{2}}=\sqrt{3}$，
所以点P的轨迹R的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$；
（2）①当直线l的斜率不为零时，设切线l的方程为x=ty+m，
∵直线l与圆O：x²+y²=1相切，∴$\frac{|m|}{\sqrt{{1}^{2}+（-t）^{2}}}=1$，
化简得，m²=1+t²，
设A（x₁，y₁），B（x₂，y₂），
由$\left\{\begin{array}{l}{x=ty+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$消去x得，（3t²+4）y²+6tmy+3m²-12=0，
∴△=（6tm）²-4（3t²+4）（3m²-12）=48（3t²-m²+4）
=48（2t²+3）＞0，
y₁+y₂=$-\frac{6tm}{3{t}^{2}+4}$，y₁y₂=$\frac{3{m}^{2}-12}{3{t}^{2}+4}$，
∴|AB|=|y₁-y₂|=$\sqrt{1+{t}^{2}}$•$\sqrt{（-\frac{6tm}{3{t}^{2}+4}）^{2}-4×\frac{3{m}^{2}-12}{3{t}^{2}+4}}$
=$4\sqrt{3}$•$\frac{\sqrt{1+{t}^{2}}•\sqrt{2{t}^{2}+3}}{3{t}^{2}+4}$，
设n=3t²+4≥4，则t²=$\frac{1}{3}（n-4）$，$0＜\frac{1}{n}≤\frac{1}{4}$，
∴|AB|=$4\sqrt{3}•\frac{\sqrt{1+\frac{1}{3}（n-4）}×\sqrt{\frac{2}{3}（n-4）+3}}{n}$=$\frac{4\sqrt{3}}{3}\sqrt{\frac{2{n}^{2}-n-1}{{n}^{2}}}$
=$\frac{4\sqrt{3}}{3}\sqrt{-\frac{1}{{n}^{2}}-\frac{1}{n}+2}$=$\frac{4\sqrt{3}}{3}\sqrt{-（\frac{1}{n}+\frac{1}{2}）^{2}+\frac{9}{4}}$，
∵$0＜\frac{1}{n}≤\frac{1}{4}$，∴$-（\frac{1}{n}+\frac{1}{2}）^{2}+\frac{9}{4}∈[\frac{27}{16}，2）$，则|AB|∈[3，$\frac{4\sqrt{6}}{3}$），
∵S_△AOB=$\frac{1}{2}$×1×|AB|=$\frac{1}{2}$|AB|，∴△AOB的面积取值范围是$[\frac{3}{2}，\frac{2\sqrt{6}}{3}）$，
②当直线l的斜率不为零时，则直线l的方程为y=±1，
代入$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$得，x=$±\frac{2\sqrt{6}}{3}$，此时|AB|=$\frac{4\sqrt{6}}{3}$，
∴S_△AOB=$\frac{1}{2}$×1×|AB|=$\frac{1}{2}$|AB|=$\frac{2\sqrt{6}}{3}$，
综上可得|，∴△AOB的面积取值范围是$[\frac{3}{2}，\frac{2\sqrt{6}}{3}]$．

点评 本题考查椭圆的定义与方程，直线与椭圆的位置关系，以及韦达定理，弦长公式，考查换元法和函数的性质，分类讨论思想、转化思想，化简变形、计算能力．