
分析 根据题意,由点P的坐标分析可得抛物线开口向上,设其标准方程为x2=2py,由P到焦点的距离为5,结合抛物线的定义可得1-(-$\frac{p}{2}$)=5,解可得p的值,将p的值代入抛物线方程即可得答案.
解答 解:根据题意,P(m,1)在x轴上方,则抛物线开口向上,
设其标准方程为x2=2py,(p>0)
其准线为y=-$\frac{p}{2}$,
P到焦点的距离为5,则有1-(-$\frac{p}{2}$)=5,
解可得p=8,
则抛物线的标准方程为x2=16y,
故答案为:x2=16y.
点评 本题考查抛物线的简单性质,考查待定系数法的应用,关键是分析抛物线的开口方向,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
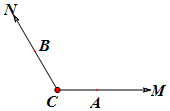 已知点A,B分别在射线CM,CN(不含端点C)上运动,$∠MCN=\frac{2π}{3}$,在△ABC中,角A,B,C所对的边分别是a,b,c.
已知点A,B分别在射线CM,CN(不含端点C)上运动,$∠MCN=\frac{2π}{3}$,在△ABC中,角A,B,C所对的边分别是a,b,c.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2n}{n+1}$ | B. | $\frac{2}{n(n+1)}$ | C. | $\frac{n(n+1)}{2}$ | D. | $\frac{n}{2(n+1)}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 虚数 | B. | 纯虚数 | C. | 实数 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2k+1 | B. | 2k+2 | C. | (2k+1)+(2k+2) | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com