
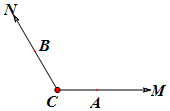
 已知点A,B分别在射线CM,CN(不含端点C)上运动,$∠MCN=\frac{2π}{3}$,在△ABC中,角A,B,C所对的边分别是a,b,c.
已知点A,B分别在射线CM,CN(不含端点C)上运动,$∠MCN=\frac{2π}{3}$,在△ABC中,角A,B,C所对的边分别是a,b,c.分析 (1)利用等差中项以及已知条件,结合余弦定理转化求解即可.
(2)利用正弦定理列出三角形的周长,通过两角和与差的三角函数结合三角函数的有界性求解即可.
解答 解:(1)因为a,b,c成等差数列,且公差为2,故a=c-4,b=c-2,
在△ABC中,$∠MCN=\frac{2π}{3}$,所以$cosC=-\frac{1}{2}$,
由余弦定理得$cosC=\frac{{{a^2}+{b^2}-{c^2}}}{2ab}=-\frac{1}{2}$;代入得c2-9c+14=0,
解得c=2或c=7;因为c>4,故c=7.
(2)在△ABC中,$C=\frac{2π}{3}$,$c=\sqrt{3}$,设∠ABC=θ,
由正弦定理得$\frac{AC}{sinθ}=\frac{BC}{{sin(\frac{π}{3}-θ)}}=\frac{ab}{{sin\frac{2π}{3}}}$,所以AC=2sinθ,$BC=2sin(\frac{π}{3}-θ)$;
设△ABC的周长为l,则$l=2sinθ+2sin(\frac{π}{3}-θ)+\sqrt{3}=2sin(θ+\frac{π}{3})+\sqrt{3}$,
因为$θ∈(0,\frac{π}{3})$,所以当$θ+\frac{π}{3}=\frac{π}{2}$,即$θ=\frac{π}{6}$时,周长l取到最大值$2+\sqrt{3}$.
点评 本题考查正弦定理以及余弦定理的应用,两角和与差的三角函数,以及三角函数的有界性的应用,考查计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 内切 | B. | 相交 | C. | 外切 | D. | 相离 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{3}$ | B. | 2 | C. | $\frac{4}{3}$ | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,3] | B. | (-∞,-3]∪[3,+∞) | C. | (-∞,-1]∪[1,+∞) | D. | [-1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{17}}}{17}$ | B. | $\frac{{3\sqrt{2}}}{5}$ | C. | $\frac{{3\sqrt{17}}}{34}$ | D. | $\frac{{2\sqrt{10}}}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com