练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设向量a＝(4cosα，sinα)，b＝(sinβ，4cosβ)，c＝(cosβ，－4sinβ)．

    (1)若a与b－2c垂直，求tan(α＋β)的值；

    (2)求|b＋c|的最大值；

    (3)若tanαtanβ＝16，求证：a∥b.


     (1)由a与b－2c垂直．a·(b－2c)＝a·b－2a·c＝0，

    即4sin(α＋β)－8cos(α＋β)＝0，tan(α＋β)＝2.

    (2)b＋c＝(sinβ＋cosβ，4cosβ－4sinβ)，

    |b＋c|2＝sin2β＋2sinβcosβ＋cos2β＋16cos2β－32cosβsinβ＋16sin2β

    ＝17－30sinβcosβ＝17－15sin2β最大值为32，

    ∴|b＋c|的最大值为4.

    (3)证明：由tanαtanβ＝16得sinαsinβ＝16cosαcosβ，

    即4cosα·4cosβ－sinαsinβ＝0，∴a∥b.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知点A(2,3)，C(0,1)，且，则点B的坐标为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设a、b是两个不共线的非零向量(t∈R)．

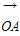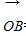    (1)记＝a，＝tb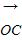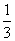，＝(a＋b)，那么当实数t为何值时，A、B、C三点共线？

    (2)若|a|＝|b|＝1且a与b夹角为120°，那么实数x为何值时，|a－xb|的值最小？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知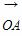＝(3，－4)，＝(6，－3)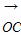，＝(5－m，－3－m)．

    (1)若点A、B、C能构成三角形，则实数m应满足的条件为________．

    (2)若△ABC为Rt△，且∠A为直角，则m＝______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若向量a与b不共线，a·b≠0，且c＝a－，则向量a与c的夹角为(　　)

    A．0                                                             B.

    C.                                                              D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在直角梯形ABCD中，AB∥CD，AD⊥AB，∠B＝45°，AB＝2CD＝2，M为腰BC的中点，则＝(　　)

    A．1　　　　B．2　　　　C．3　　　　D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    直线ax＋by＋c＝0与圆x2＋y2＝9相交于两点M、N，若c2＝a2＋b2，则(O为坐标原点)等于(　　)

    A．－7  B．－14  C．7  D．14

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在平行四边形ABCD中，∠BAD＝60°，AD＝2AB，若P是平面ABCD内一点，且满足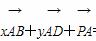＝0(x，y∈R)，则当点P在以A为圆心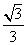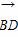，||为半径的圆上时，实数x，y应满足关系式为(　　)

    A．4x2＋y2＋2xy＝1                                       B．4x2＋y2－2xy＝1

    C．x2＋4y2－2xy＝1                                       D．x2＋4y2＋2xy＝1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设Sn表示等差数列{an}的前n项和，已知＝，那么等于(　　)

    A.  B.  C.  D.

    查看答案和解析>>

    同步练习册答案