练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．已知{an}为等比数列．
    （1）若an＞0，a2a4+2a3a5+a4a6=25，求a3+a5；
    （2）若an＞0，a5a6=9，求log3a1+log3a2+…+log3a10的值．

    分析 （1）由已知式子和等比数列的性质可得a32+2a3a5+a52=25即（a3+a5）2=25，解方程可得；
    （2）由题意和等比数列的性质以及对数的运算可得原式=log3（a5a6）5，代值计算可得．

    解答 解：（1）∵{an}为等比数列，且an＞0，a2a4+2a3a5+a4a6=25，
    ∴a32+2a3a5+a52=25，故（a3+a5）2=25，解得a3+a5=5；
    （2）∵an＞0且a5a6=9，
    ∴log3a1+log3a2+…+log3a10
    =log3a1a2…a10=log3（a5a6）5=log395=log3310=10．

    点评 本题考查等比数列的通项公式和性质，涉及对数的运算性质，属基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    10．已知集合A={x|y=lg（a-x）}，B={x|1＜x＜2}，且（∁RB）∪A=R，则实数a的取值范围是[2，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．“sinα=0”是“cosα=1”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充分必要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知x，y满足约束条件$\left\{\begin{array}{l}{x+y=10}\\{x≥0}\\{y≥0}\end{array}\right.$，则目标函数z=3x+3y的最大值为30，该线性规划有无数个最优解．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知锐角三角形的边长分别为2，4，x，则x的取值范围是（　　）
    A．（1，$\sqrt{5}$）B．（$\sqrt{5}$，$\sqrt{13}$）C．（1，2$\sqrt{5}$）D．（2$\sqrt{3}$，2$\sqrt{5}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．函数f（x）=asin（2x+φ）+cos（2x+φ），（a＞0，|φ|＜$\frac{π}{2}$）的最大值为2，且f（-x）=f（x），则a，φ的取值分别为（　　）
    A．a=1，φ=$\frac{π}{3}$B．a=1，φ=$\frac{π}{6}$C．a=$\sqrt{3}$，φ=$\frac{π}{3}$D．a=$\sqrt{3}$，φ=$\frac{π}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．a∈R，设函数f（x）=（-x2+ax）e-x，x∈R．
    （1）当a=-2时，求函数f（x）的单调减区间；
    （2）若x∈（-1，1）内单调递减，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

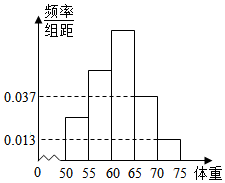    18．为了解今年某校高三毕业班准备报考飞行员学生的体重情况，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，其中第2小组的频数为12．
    （Ⅰ）求该校报考飞行员的总人数；
    （Ⅱ）以这所学校的样本数据来估计全省的总体数据，若从全省报考飞行员的同学中（人数很多）任选三人，设X表示体重超过60公斤的学生人数，求X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．设椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别是F1，F2，P为椭圆C上的点，在△PF1F2中，点Q满足$\overrightarrow{{F}_{1}P}$=4$\overrightarrow{{F}_{1}Q}$，∠F1PF2=∠QF2F1，则椭圆C的离心率e的取值范围是（　　）
    A．0＜e＜$\frac{1}{5}$B．$\frac{1}{5}$＜e＜$\frac{1}{3}$C．$\frac{1}{3}$＜e＜1D．0＜e＜$\frac{1}{5}$或$\frac{1}{3}$＜e＜1

    查看答案和解析>>

    同步练习册答案