
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由于$α=\frac{1}{2}+\frac{{\sqrt{3}}}{2}i,β=-\frac{1}{2}-\frac{{\sqrt{3}}}{2}i$,
对于①,可求得αβ=$\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i≠1,可判断①错误;
对于②,可求得$\frac{α}{β}=-1$,可判断②错误;
对于③,可求得$|{\frac{α}{β}}|=1$,可判断③正确;
对于④,可求得α2+β2=-1+$\sqrt{3}$i≠1,可判断④错误.
解答 解:$α=\frac{1}{2}+\frac{{\sqrt{3}}}{2}i,β=-\frac{1}{2}-\frac{{\sqrt{3}}}{2}i$,
对于①,αβ=-($\frac{1}{4}$+$\frac{\sqrt{3}}{2}$i-$\frac{3}{4}$)=$\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i≠1,故①错误;
对于②,$\frac{α}{β}$=$\frac{\frac{1}{2}+\frac{\sqrt{3}}{2}i}{-\frac{1}{2}-\frac{\sqrt{3}}{2}ii}$=-1≠1,故②错误;
对于③,$|\frac{α}{β}|$=$\frac{|α|}{|β|}$=$\frac{\sqrt{{(\frac{1}{2})}^{2}{+(\frac{\sqrt{3}}{2})}^{2}}}{\sqrt{{(-\frac{1}{2})}^{2}{+(-\frac{\sqrt{3}}{2})}^{2}}}$=1,故③正确;
对于④,α2+β2=($\frac{1}{4}$+$\frac{\sqrt{3}}{2}$i-$\frac{3}{4}$)+($\frac{1}{4}$+$\frac{\sqrt{3}}{2}$i-$\frac{3}{4}$)=-1+$\sqrt{3}$i≠1,故④错误.
综上所述,正确的个数为1个,
故选:A.
点评 本题考查命题的真假判断与应用,突出考查复数的乘法、除法、乘方运算及复数求模,属于中档题.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | [0,5] | B. | [1,5] | C. | (0,5) | D. | [1,25] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
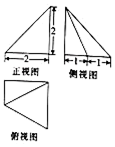
| A. | $12+\sqrt{3}$ | B. | $10+\sqrt{3}$ | C. | $10+2\sqrt{3}$ | D. | $11+\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11 | B. | 10 | C. | 6 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,-1) | B. | (1,-1) | C. | (-1,1) | D. | (1,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com