
分析 设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),与圆方程为x2+y2=c2,联立方程组,解得x,y,由题意可得c>b,再由离心率公式,计算即可得到所求范围.
解答 解:设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
以原点为圆心,椭圆的焦半径c为半径的圆方程为x2+y2=c2,
联立两方程,可得y2=$\frac{{b}^{2}({a}^{2}-{c}^{2})}{{a}^{2}-{b}^{2}}$,x2=$\frac{{a}^{2}({c}^{2}-{b}^{2})}{{a}^{2}-{b}^{2}}$,
由题意可得x2>0,y2>0,
结合a>b>0,a>c>0,可得c2>b2,
即有c2>a2-c2,即为a<$\sqrt{2}$c,
则离心率e=$\frac{c}{a}$>$\frac{\sqrt{2}}{2}$,由0<e<1,可得
$\frac{\sqrt{2}}{2}$<e<1.
故答案为:($\frac{\sqrt{2}}{2}$,1).
点评 本题考查椭圆的离心率的范围,注意运用圆与椭圆方程联立,通过方程组有解,考查运算能力,属于中档题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:解答题
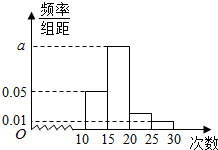 某校对高一年级学生暑假参加社区服务的次数进行了统计,随机抽取了M名学生作为样本,得到这M名学生参加社区服务的次数,根据此数据作出了频率分布统计表和频率分布直方图如下:
某校对高一年级学生暑假参加社区服务的次数进行了统计,随机抽取了M名学生作为样本,得到这M名学生参加社区服务的次数,根据此数据作出了频率分布统计表和频率分布直方图如下:| 分组 | 频数 | 频率 |
| [10,15) | 10 | 0.25 |
| [15,20) | 25 | n |
| [20,25) | m | p |
| [25,30) | 2 | 0.05 |
| 合计 | M | N |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | B. | $\frac{x^2}{12}-\frac{y^2}{4}=1$ | C. | $\frac{y^2}{4}-\frac{x^2}{12}=1$ | D. | $\frac{y^2}{12}-\frac{x^2}{4}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com